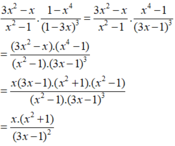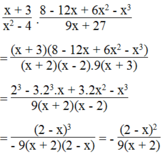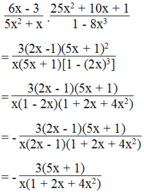Nêu quy tắc rút gọn biểu thức ( lớp 7,8)

Những câu hỏi liên quan
Nêu quy tắc rút gọn biểu thức
Biểu thức hay đa thức z?
biểu thức lớp 7,8 á
Muốn rút gọn một phân thức đại số ta phải:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung giống nhau.
Chú ý: Đôi khi cần đổi dấu tử hoặc mẫu thức để xuất hiện nhân tử chung.
Cre: loigiaihay
Xem thêm câu trả lời
Nêu các tính chất cơ bản của phân số? Thế nào là phân số tối giản? Phát biểu quy tắc quy đồng mẫu số nhiều phân số, quy tắc rút gọn phân số? Để so sánh hai phân số ta làm thế nào?
- Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được phân số bằng phân số đã cho.
\(\frac{a}{b}=\frac{a.m}{b.m}\Leftrightarrow m\in Z,m\ne0\)
Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
\(\frac{a}{b}=\frac{a:n}{b:n}\Leftrightarrow n\in UC\left(a;b\right)\)
Lưu ý:
Nếu ta nhân cả tử và mẫu của một phân số với -1 thì ta được một phân số bằng nó có tử và mẫu lần lượt là đối số của tử số và mẫu số của phân số đã cho.
Nói cách khác, nếu ta đổi dấu cả tử và mẫu của một phân số thì được phân số bằng phân số đã cho.
- Phân số tối giản là phân số mà có tử số và mẫu số không thể cùng chia hết cho số nào ngoại trừ số 1 ( hoặc -1 nếu lấy các số âm ). Nói cách khác phân số là tối giản nếu a và b là nguyên tố cùng nhau, nghĩa là a và b có ước số chung lớn nhất là 1.
- Muốn quy đồng mẫu số nhiều phân số với mẫu số dương ta làm như sau:
Bước 1: Tìm bội chung của các mẫu ( thường là bội chung nhỏ nhất ( BCNN ) để làm mẫu chung ).
Bước 2: Tìm thừa số phụ của mỗi mẫu ( bằng cách chia mẫu chung cho từng mẫu ).
Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
- Muốn rút gọn phân số ta chia cả tử và mẫu của phân số cho một ước chung khác 1 và - 1 của chúng.
- 1. So sánh hai phân số cùng mẫu.
Trong hai phân số cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
2. So sánh hai phân số không cùng mẫu
Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng mẫu dương rồi so sánh các tử với nhau.
Lưu ý:
* Phân số nào có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0. Phân số lớn hơn 0 được gọi là phân số dương.
* Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn 0. Phân số nhỏ hơn 0 được gọi là phân số âm.
Kiên trì!
Nêu các tính chất cơ bản của phân số? Thế nào là phân số tối giản? Phát biểu quy tắc quy đồng mẫu số nhiều phân số, quy tắc rút gọn phân số? Để so sánh hai phân số ta làm thế nào?
Mình giúp bạn mấy câu này rồi đấy!
Xem thêm câu trả lời
Nêu quy tắc rút gọn một phân thức đại số.
Hãy rút gọn phân thức :
\(\dfrac{8x-4}{8x^3-1}\)
Muốn rút gọn phân thức đại số ta có thể :
+ Phân tích tử và mẫu thành nhân tử ( nếu cần ) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung.
Rút gọn phân thức :
\(\dfrac{8x-4}{8x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{2x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(2x^2+2x+1\right)}\)\(=\dfrac{4}{4x^2+2x+1}\)
Đúng 0
Bình luận (0)
*Quy tắc rút gọn một phân thức đại số là:
-Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
-Chia cả tử và mẫu cho nhân tử chung.
*Bài tập:
\(\dfrac{8x-4}{8x^3-1}=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(x^2+x+1\right)}=\dfrac{4}{x^2+x+1}\)
Đúng 0
Bình luận (0)
Quy tắc rút gọn một phân thức đại số là:
1.Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
2.Chia cả tử và mẫu cho nhân tử chung.
Giải bài tập:
\(\dfrac{8x-4}{8x^3-1}\) = \(\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(4x^2+2x+1\right)}\) = \(\dfrac{4}{4x^2+2x+1}\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung)
3
x
2
-
x
x
2
-
1
.
1
-
x
4
1
-
3
x...
Đọc tiếp
Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung) 3 x 2 - x x 2 - 1 . 1 - x 4 1 - 3 x 3
Nêu qui tắc rút gọn một phân thức đại số. Hãy rút gọn phân thức
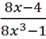
Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn:
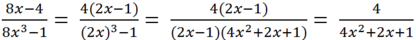
Đúng 0
Bình luận (0)
Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung)
x
+
3
x
2
-
4
.
8
-
12
x
+
6
x
2
-
x...
Đọc tiếp
Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung) x + 3 x 2 - 4 . 8 - 12 x + 6 x 2 - x 3 9 x + 27
Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung)
6
x
-
3
5
x
2
+
x
.
25
x
2
+
10
x
+
1...
Đọc tiếp
Rút gọn các biểu thức (chú ý dùng quy tắc đổi dấu để thay nhân tử chung) 6 x - 3 5 x 2 + x . 25 x 2 + 10 x + 1 1 - 8 x 3
Câu 2: Áp dụng quy tắc dấu ngoặc để rút gọn biểu thức:
a) A = 23 - x - (x - 46) + 2x - 43
b) B = - (4 - 2x) + [ 76 - x - (x + 99)]
\(A=23-x-x+46+2x-43=26\)
\(B=-4+2x+76-x-x-99=-27\)
Đúng 0
Bình luận (1)