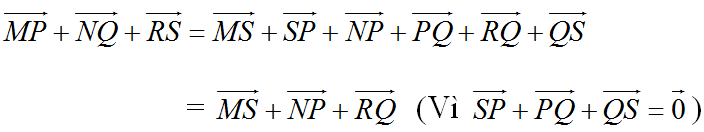CHo 3 điểm M,N,P thõa mãn \(\overrightarrow{MN}=-2\overrightarrow{MP}\) . Gọi O là điểm bất kì.

Những câu hỏi liên quan
Cho ΔABC trọng tâm G , gọi I là trung điểm BC . Tìm M là điểm thõa mãn \(2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Do G là trọng tâm ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Do I là trung điểm BC \(\Rightarrow\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}\)
\(2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow2\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=3.\left|2\overrightarrow{MI}\right|\)
\(\Leftrightarrow2.\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=6\left|\overrightarrow{MI}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MG}\right|=6\left|\overrightarrow{MI}\right|\)
\(\Leftrightarrow MG=MI\)
Tập hợp M là đường trung trực của đoạn thẳng IG
Đúng 1
Bình luận (0)
Cho ΔABC. Gọi 2 điểm M, N thay đổi và thỏa mãn:
\(\overrightarrow{MN}=2\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\)
Chứng minh MN luôn đi qua 1 điểm cố định
Cho 6 điểm M, N, P, Q, R, S bất kì. Chứng minh rằng :
\(\overrightarrow{MP}+\overrightarrow{NQ}+\overrightarrow{RS}=\overrightarrow{MS}+\overrightarrow{NP}+\overrightarrow{RQ}\)
Cho tam giác đều ABC, tâm O. M là một điểm bất kì trong tam giác. Hình chiếu vuông góc của M xuống 3 cạnh của tam giác là D, E, F. Từ M kẻ ba đường thẳng song song với 3 cạnh của tam giác. Các giao điểm với các cạnh lần lượt là: I, J, K, L, P, Q (D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ). Chứng minh:overrightarrow{MD}frac{overrightarrow{MI}+overrightarrow{MQ}}{2};overrightarrow{ME}frac{overrightarrow{MK}+overrightarrow{MP}}{2};overrightarrow{MF}frac{overrigh...
Đọc tiếp
Cho tam giác đều ABC, tâm O. M là một điểm bất kì trong tam giác. Hình chiếu vuông góc của M xuống 3 cạnh của tam giác là D, E, F. Từ M kẻ ba đường thẳng song song với 3 cạnh của tam giác. Các giao điểm với các cạnh lần lượt là: I, J, K, L, P, Q (D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ). Chứng minh:
\(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\);\(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\);\(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
Bạn xem lại đề ạ!
Nếu bạn đã chứng minh được D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ
Thì dễ dàng suy ra được: \(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\); \(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\); \(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
( Vì chúng ta có tính chất: Nếu I là trung điểm đoạn thẳng AB thì mọi điểm M ta có: \(2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}\))
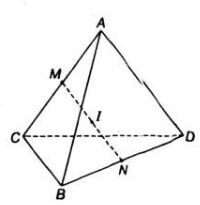
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh :
a) overrightarrow{IA}+overrightarrow{IB}+overrightarrow{IC}+overrightarrow{ID}overrightarrow{0}
b) overrightarrow{PI}dfrac{1}{4}left(overrightarrow{PA}+overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PD}right)
Đọc tiếp
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh :
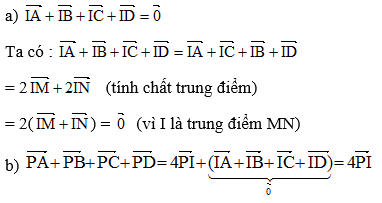
a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
b) \(\overrightarrow{PI}=\dfrac{1}{4}\left(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}\right)\)
Cho ΔABC . Tìm tập hợp điểm M thõa mãn \(\left|3\overrightarrow{MA}+2\overrightarrow{MB}-2\overrightarrow{MC}\right|=\left|\overrightarrow{MB}-\overrightarrow{MC}\right|\)
Qua A dựng đường thẳng d song song BC, trên d lấy điểm I sao cho \(\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{BC}\)
\(\Rightarrow3\overrightarrow{IA}=2\overrightarrow{BC}\Rightarrow3\overrightarrow{IA}+2\overrightarrow{CB}=\overrightarrow{0}\)
Ta có:
\(\left|3\overrightarrow{MA}+2\overrightarrow{MB}-2\overrightarrow{MC}\right|=\left|\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MA}+2\left(\overrightarrow{MB}+\overrightarrow{CM}\right)\right|=\left|\overrightarrow{MB}+\overrightarrow{CM}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MA}+2\overrightarrow{CB}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MI}+3\overrightarrow{IA}+2\overrightarrow{CB}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MI}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow MI=\dfrac{1}{3}BC\)
Tập hợp M là đường tròn tâm I bán kính \(\dfrac{BC}{3}\)
Đúng 1
Bình luận (0)
câu 1: cho tứ giác ABCD. Gọi O là trung điểm của AB.Chứng minh rằng: overrightarrow{OD}+overrightarrow{OC}overrightarrow{AD}+overrightarrow{BC}Câu 2: Cho tam giác ABC. Gọi A là điểm đối xứng của B qua A, B là điểm dối xứng của C qua B, C là điểm đối xứng của A qua C. Với một điểm O bất kì, chứng minh rằng:overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}
Đọc tiếp
câu 1: cho tứ giác ABCD. Gọi O là trung điểm của AB.
Chứng minh rằng: \(\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{AD}+\overrightarrow{BC}\)
Câu 2: Cho tam giác ABC. Gọi A' là điểm đối xứng của B qua A, B' là điểm dối xứng của C qua B, C' là điểm đối xứng của A qua C. Với một điểm O bất kì, chứng minh rằng:
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}\)
câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
Đúng 0
Bình luận (0)
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Khẳng định nào sau đây là đúng:A. overrightarrow{MN}overrightarrow{CP} và overrightarrow{MP}overrightarrow{NC} B. overrightarrow{MN}overrightarrow{CP} và overrightarrow{MP}overrightarrow{NC}C. overrightarrow{MN}overrightarrow{CP} và overrightarrow{MP}overrightarrow{CN} D. overrightarrow{MN}overrightarrow{CP} và overrightarrow{M...
Đọc tiếp
Cho tam giác ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Khẳng định nào sau đây là đúng:
A. \(\overrightarrow{MN}=\overrightarrow{CP}\) và \(\overrightarrow{MP}=\overrightarrow{NC}\) B. \(\overrightarrow{MN}=\overrightarrow{CP}\) và \(\overrightarrow{MP}=\overrightarrow{NC}\)
C. \(\overrightarrow{MN}=\overrightarrow{CP}\) và \(\overrightarrow{MP}=\overrightarrow{CN}\) D. \(\overrightarrow{MN}=\overrightarrow{CP}\) và \(\overrightarrow{MP}=\overrightarrow{CN}\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\overrightarrow{PC}\\\overrightarrow{MP}=\overrightarrow{NC}\\\overrightarrow{PN}=\overrightarrow{MB}\end{matrix}\right.\)
Bạn xem lại nha, có thể đáp án A hoặc B sẽ có \(\overrightarrow{MN}=\overrightarrow{PC}\)
Đúng 0
Bình luận (1)
Bài 1: Cho 4 điểm A, B,C,D bất kì. Gọi M,N lần lượt là trung điểm của AC và BD. Chứng minh rằng overrightarrow{AB} +overrightarrow{CD} 2overrightarrow{MN}
Bài 2: Cho 4 điểm A, B,C,D bất kì và M,N lần lượt là trung điểm của AB và CD. G là trung điểm MN. Chứng minh rằng:
a, overrightarrow{GA} +overrightarrow{GB} +overrightarrow{GC} + overrightarrow{GD} overrightarrow{0}
b, Với mọi điểm O ta đều có: overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}+overrightarrow{OD} 4overrightarrow{OG...
Đọc tiếp
Bài 1: Cho 4 điểm A, B,C,D bất kì. Gọi M,N lần lượt là trung điểm của AC và BD. Chứng minh rằng \(\overrightarrow{AB}\) +\(\overrightarrow{CD}\) = 2\(\overrightarrow{MN}\)
Bài 2: Cho 4 điểm A, B,C,D bất kì và M,N lần lượt là trung điểm của AB và CD. G là trung điểm MN. Chứng minh rằng:
a, \(\overrightarrow{GA}\) +\(\overrightarrow{GB}\) +\(\overrightarrow{GC}\) + \(\overrightarrow{GD}\) = \(\overrightarrow{0}\)
b, Với mọi điểm O ta đều có: \(\overrightarrow{OA}\)+\(\overrightarrow{OB}\)+\(\overrightarrow{OC}\)+\(\overrightarrow{OD}\)= 4\(\overrightarrow{OG}\)
Bài 3: Cho ngũ giác ABCDE. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD,DE. Gọi I,J lần lượt là trung điểm của MP và NQ. Chứng minh rằng \(\overrightarrow{IJ}\)= \(\overset{1}{4}\) \(\overrightarrow{AE}\)
cô nàng ma kết ơi sao mà tên kì cục thế cô nàng.
Xem thêm câu trả lời