hình tam giác,ngôi sao,hình thoi có tâm đối xứng không
Những câu hỏi liên quan
TRong các hình sau hình nào không có trục đối xứng và tâm đối xứng : tam giác, tam giác cân, tam giác đều, hình thang, hình thang cân, hình vuông, hình chữ nhật, hình thoi
giúp mk vs các bn . tks ạ!!1 :))
Câu 26. Hình nào sau đây không có tâm đối xứng ? A. Hình lục giác đều B. Tam giác đều C. Hình thoi
Câu 25. Trong các hình sau, hình nào không có trục đối xứng ? A. Hình thang cân B. Hình bình hành C. Hình vuông D. Hình chữ nhật
Câu 26. Hình nào sau đây không có tâm đối xứng ? A. Hình lục giác đều B. Tam giác đều C. Hình thoi
Tính diện tích hình bình hành có độ dài đáy là 25dm và chiều cao là 18dm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
22 tháng 10 2021 lúc 18:52
Trong các hình: đoạn thẳng; đường tròn; tam giác đều; hình thang cân; hình bình hành; hình vuông; hình thoi; hình chữ nhật; lục giác đều, hình nào không có tâm đối xứng?
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của hai đường chéo.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của hai đường chéo.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.
Máy in laser màu HP
Máy in laser màu Canon
Máy in laser đa chức năng
Máy in laser đen trắng
Đúng 0
Bình luận (0)
đường thẳng,tam giác, tam giác cân, tam giác đều, tứgiác, hình thang, hình thang cân, hình bình hành, hình chữnhật, hình thoi, hình tròn có bao nhiêu trục và tâm đối xứng
28 tháng 11 2018 lúc 20:32
Các tứ giác sau có bao nhiêu trục đối xứng, bao nhiêu tâm đối xứng?Tứ giác: ___ trục đối xứng, ___ tâm đối xứngHình thang: ___ trục đối xứng, ___ tâm đối xứngHình thang cân: ___ trục đối xứng, ___ tâm đối xứngHình binh hành: ___ trục đối xứng, ___ tâm đối xứngHình chữ nhật: ___ trục đối xứng, ___ tâm đối xứngHình thoi: ___ trục đối xứng, ___ tâm đối xứngHình vuông: ___ trục đối xứng, ___ tâm đối xứng
Đọc tiếp
Các tứ giác sau có bao nhiêu trục đối xứng, bao nhiêu tâm đối xứng?
Tứ giác: ___ trục đối xứng, ___ tâm đối xứng
Hình thang: ___ trục đối xứng, ___ tâm đối xứng
Hình thang cân: ___ trục đối xứng, ___ tâm đối xứng
Hình binh hành: ___ trục đối xứng, ___ tâm đối xứng
Hình chữ nhật: ___ trục đối xứng, ___ tâm đối xứng
Hình thoi: ___ trục đối xứng, ___ tâm đối xứng
Hình vuông: ___ trục đối xứng, ___ tâm đối xứng
Tứ giác: 0 trục, 0 tâm
Hình thang 0 trục, 0 tâm
Hình thang cân 1 trục 0 tâm
Hình bình hành 0 trục 1 tâm
Hình chữ nhật 2 trục 1 tâm
Hình thoi 2 trục 1 tâm
Hình vuông 4 trục 1 tâm
Đúng 2
Bình luận (0)
Tứ giác: 0 trục đối xứng, 0 tâm đối xứng
Hình thang: 0 trục đối xứng, 0 tâm đối xứng
Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng
Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng
Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng
Hình thoi: 2 trục đối xứng, 1 tâm đối xứng
Hình vuông: 4 trục đối xứng, 1 tâm đối xứng
Tích đúng 5 sao cho mình nhé.
OK bạn
Đúng 2
Bình luận (0)
1.Trong các câu sau, câu nào sai?
a.Hinhd lục giác đều có 6 tâm đối xứng.
b.Hình thoi có tâm đối xứng là giao điểm của hai đường chéo.
c.Hình vuông có tâm đối xứng là tâm của hình tròn.
d.Hình tròn có tâm đối xứng là tâm của hình tròn.
2.Hình chữ nhật có mấy trục đối xứng
Xem thêm câu trả lời
Em hãy cho biết trong những hình đã học như hình vuông, hình tam giác đều, hình lục giác đều, hình chữ nhật, hình bình hành, hình thoi, hình thang cân, hình nào có tâm đối xứng.
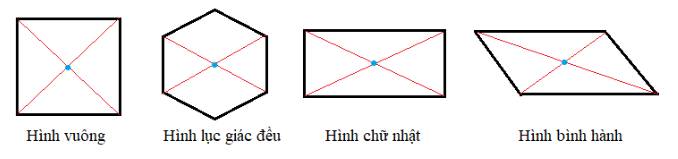
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.
Đúng 0
Bình luận (0)
Trong các hình hình học sau: đoạn thẳng, đường thẳng, tam giác, tam giác cân, tam giác đều, tứgiác, hình thang, hình thang cân, hình bình hành, hình chữnhật, hình thoi, hình tròn thì:a) Những hình hình học nào có tâm đối xứng?b) Những hình hình học nào có trục đối xứng?c) Những hình hình học nào vừa có tâm đối xứng, vừa có trục đối xứng?
Đọc tiếp
Trong các hình hình học sau: đoạn thẳng, đường thẳng, tam giác, tam giác cân, tam giác đều, tứgiác, hình thang, hình thang cân, hình bình hành, hình chữnhật, hình thoi, hình tròn thì:
a) Những hình hình học nào có tâm đối xứng?
b) Những hình hình học nào có trục đối xứng?
c) Những hình hình học nào vừa có tâm đối xứng, vừa có trục đối xứng?
)Trong các hình hình học sau: đoạn thẳng, đường thẳng, tam giác, tam giác cân, tam giác đều, tứgiác, hình thang, hình thang cân, hình bình hành, hình chữnhật, hình thoi, hình tròn thì:a) Những hình hình học nào có tâm đối xứng?b) Những hình hình học nào có trục đối xứng?c) Những hình hình học nào vừa có tâm đối xứng, vừa có trục đối xứng?
Đọc tiếp
)Trong các hình hình học sau: đoạn thẳng, đường thẳng, tam giác, tam giác cân, tam giác đều, tứgiác, hình thang, hình thang cân, hình bình hành, hình chữnhật, hình thoi, hình tròn thì:a) Những hình hình học nào có tâm đối xứng?b) Những hình hình học nào có trục đối xứng?c) Những hình hình học nào vừa có tâm đối xứng, vừa có trục đối xứng?