Tìm min, max
5x-2x2+1
Tìm GTLN (max), GTNN (min) của y = 2 x 2 - 3 x + 9 x - 1 trên 2 ; 4
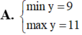
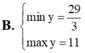
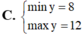
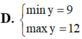
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x 2 + 1 trên - 1 ; 1
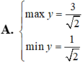
cho các số dương x,y,z thỏa mãn x+y+z=1 tìm min của biểu thức
P=√(2x2+xy+2y2) +√(2y2+yz+2z2)+ √(2z2+xz+2x2)
Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737
tìm min của 2x2 + 3xyz + 2z2 + xy + yz + xz + y2 +2020
Tìm Min/Max
A= y2-4y+9
B=x2-x+1
C=2x2-6x
A = y^2 - 4y + 9 = y^2 - 4y + 4 + 5
= ( y - 2 )^2 + 5 >= 5
Dấu ''='' xảy ra khi y = 2
Vậy GTNN A là 5 khi y = 2
B = x^2 - x + 1 = x^2 - x + 1/4 + 3/4 = ( x - 1/2 )^2 + 3/4 >= 3/4
Dấu ''='' xảy ra khi x = 1/2
Vậy GTNN B là 3/4 khi x = 1/2
C = 2x^2 - 6x = 2 ( x^2 - 3x + 9 / 4 - 9/4 )
= 2 ( x - 3/2 )^2 - 9/2 >= -9/2
Dấu ''='' xảy ra khi x = 3/2
Vậy GTNN C là -9/2 khi x = 3/2
a) Ta có: \(A=y^2-4y+9\)
\(=y^2-4y+4+5\)
\(=\left(y-2\right)^2+5\ge5\forall y\)
Dấu '=' xảy ra khi y=2
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Tìm GTLN (max), GTNN (min) của hàm số y = x 3 - 2 x 2 - 4 x + 8 khi x ∈ - 1 ; 1
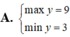
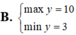
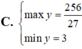
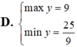
Bài 1: Giải phương trình:
a) 2x2-6=0
b)x3-5x2+6x=0
c) \(\dfrac{3}{x-1}+\dfrac{2}{x^{2^{ }}+x+1}=\dfrac{3x^2}{x^3-1}\)
Bài 2: Tìm MIN của
A=\(\dfrac{2}{-x^2-2x-2}\)
Bài 2:
\(A=\dfrac{2}{-x^2-2x-2}=\dfrac{-2\left(-x^2-2x-2\right)-2x^2-4x-2}{-x^2-2x-2}\) \(=-2+\dfrac{2\left(x+1\right)^2}{-x^2-2x-2}\ge-2\)
Dấu bằng xảy ra \(\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy \(A_{Min}=-2\) khi \(x=-1\)
Bài 1:
a) Ta có: \(2x^2-6=0\)
\(\Leftrightarrow2x^2=6\)
\(\Leftrightarrow x^2=3\)
hay \(x\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
Vậy: \(S=\left\{\sqrt{3};-\sqrt{3}\right\}\)
cho pt X^2-(2m+4)X+1=0
Tìm min A=(X1-2X2)(X1-X2)
Bài 1:
a) Tìm x, biết: 3.(x - 1) - (x + 1) = - 1
b) Tìm nghiệm của đa thức: f(x) = 2x2 - x
Bài 2:
Cho đa thức f(x) = 2x2 - 3x + x + 1 ; g(x) = 3x - 3x3 + 2x2 - 2 ;
h(x) = 2x2 + 1
a) Tính g(x) - f(x) + h(x)
b)Tính f(- 1) - h(1/2)
c) Với giá trị nào của x thì f(x) = h(x)
Bài 3:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi AD là tia phân giác của góc HAC, M là trung điểm của AD. Trên nửa mặt phẳng bờ AC chứa điểm B vẽ tia Ax song song với BC. Trên Ax lấy điểm E sao cho AE = DC
a) Chứng minh tam giác ADC = tam giác DAE
b) Chứng minh tam giác ABD là tam giác cân
c) Gọi I là giao điểm của DE và AH ; K là giao điểm của DE và AB. Chứng minh 3 điểm B, I, M thẳng hàng ?
ĐANG CẦN GẤP ! MONG MỌI NGƯỜI GIÚP ĐỠ ! CẢM ƠN RẤT NHIỀU !
Tìm min : E = 3x2−4xy+2y2−3x+20123x2−4xy+2y2−3x+2012
C = x2−x+2012(x−2)2x2−x+2012(x−2)2
D = 4x+3x2+14x+3x2+1
A = x+1+1x−1x+1+1x−1 biết rằng x > 1