x ²+y ²-3x+2y+3.Tìm giá trị lớn nhất

Những câu hỏi liên quan
Cho x^2+y^2=56. Tìm giá trị lớn nhất của |3x+2y|
x,y thỏa mãn 3x+2y=5. tìm giá trị lớn nhất E =xy
3x+2y=5 => y = (5-3x)/2
E=xy = x(5-3x)/2
=> 2E=5x-3x2 = -3(x2-5x/3)
=> \(2E=-3\left(x^2-2.\frac{5}{6}x+\frac{25}{36}-\frac{25}{36}\right)\)
=> \(2E=\frac{25}{12}-3\left(x-\frac{5}{6}\right)^2\)
Nhận thấy: \(\left(x-\frac{5}{6}\right)^2\ge0\) Với mọi x
=> Giá trị lớn nhất của 2E là 25/12, đạt được khi x=5/6
=> \(E_{min}=\frac{25}{24}\) đạt được khi x=5/6
Đúng 0
Bình luận (0)
Cho hai số thực x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
Cho hai số thực x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = x + 2 y + 3 x + y + 6
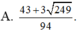
![]()
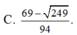
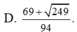
1/ cho \(^{5x^2+y^2+4xy+4x+4y-1=0}\)
tìm giá trị lớn nhất của S=2x+y-2 và giá trị x,y
2/cho \(x^2+2xy+7.\left(x+y\right)+2y^2+10=0\)
tìm giá trị lớn nhất của S=x+y+1 và giá trị x,y
3/ cho \(3x^2+y^2+2xy+4=7x+3y\)
tìm giá trị lớn nhất của S=x+y+1
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất Pmax của P = 3 x + 2 y + 1 x + y + 6 .
A. 3.
B. 2.
C. 1.
D. 4.
Đáp án C.
Ta có

Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ log 3 x + y - log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ , có f ' t = 1 + 1 t ln 3 > 0 ; ∀ t > 0 .
Suy ra f(t) là hàm số đồng biến trên 0 ; + ∞ mà f[3(x + y)] = f(x2 + y2 + xy + 2)

Đúng 0
Bình luận (0)
Xét các số thực dương x,y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
−
3...
Đọc tiếp
Xét các số thực dương x,y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x − 3 + y y − 3 + x y . Tìm giá trị lớn nhất P m a x của P = 3 x + 2 y + 1 x + y + 6 .
A. 3
B. 2
C. 1
D. 4
Đáp án C.
Ta có x x − 3 + y y − 3 + x y
= x 2 + y 2 + x y − 3 x − 3 y = x 2 + y 2 + x y + 2 − 3 x + y − 2
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ log 3 x + y − log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ ,
có f ' t = 1 + 1 t ln 3 > ; ∀ t > 0.
Suy ra f( t) là hàm số đồng biến trên 0 ; + ∞
mà f 3 x + y = f x 2 + y 2 + x y + 2
⇔ 2 x + y 2 − 6 2 x + y + 5 = − 3 y − 1 2 ≤ 0 ⇔ 1 ≤ 2 x + y ≤ 5.
Khi đó P = 1 + 2 x + y − 5 x + y + 6 ≤ 1
vì 2 x + y − 5 ≤ 0 x + y + 6 > 0 . Vậy P m a x = 1.
Đúng 0
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
log
5
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 5 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
A. m a x P = 1
B. m a x P = 4
C. m a x P = 2
D. m a x P = 3
Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
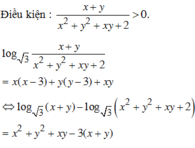
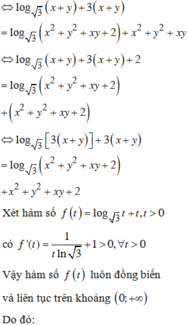
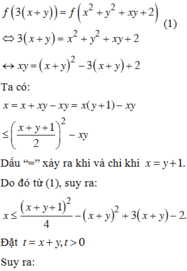
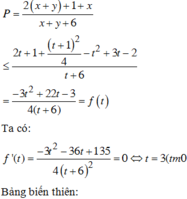
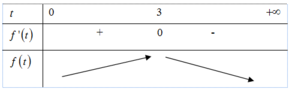


Đúng 0
Bình luận (0)
Bài 1:Tìm Giá trị nhỏ nhất
A=3(x+1)^2+5
B=2|x+y|+3x^2-10
C=12(x-y)^2 +x^2-6
D= -5/2^2+1
Bài 2:Tìm Giá trị lớn nhất
A=5-2x
B=3-(x+1)^2-3(x+2y)^2
C=-12-3|x+1|-2(y-1)^2
D=5/2x^2-3
F=-5/3-2x^2
Bài 1:
A = 3(x + 1)2 + 5
Ta có: (x + 1)2 \(\ge\) 0 Với mọi x
\(\Rightarrow\) 3(x + 1)2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 3(x + 1)2 + 5 \(\ge\) 5 với mọi x
Hay A \(\ge\) 5
Dấu "=" xảy ra khi và chỉ khi x + 1 = 5 hay x = -1
Vậy...
B = 2|x + y| + 3x2 - 10
Ta có: 2|x + y| \(\ge\) 0 với mọi x, y
3x2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 2|x + y| + 3x2 - 10 \(\ge\) -10 với mọi x,y
Dấu "=" xảy ra khi và chỉ khi x + y = 0; x = 0
\(\Rightarrow\) x = y = 0
Vậy ...
C = 12(x - y)2 + x2 - 6
Ta có: 12(x - y)2 \(\ge\) 0 với mọi x; y
x2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 12(x - y)2 + x2 - 6 \(\ge\) -6 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x = y = 0
Phần D ko rõ đầu bài nha vì D luôn có một giá trị duy nhất
Bài 2:
Phần A ko rõ đầu bài!
B = 3 - (x + 1)2 - 3(x + 2y)2
Ta có: -(x + 1)2 \(\le\) 0 với mọi x
-3(x + 2y)2 \(\le\) 0 với mọi x, y
\(\Rightarrow\) 3 - (x + 1)2 - 3(x + 2y)2 \(\le\) 3 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x = 2y; x + 1 = 0
\(\Rightarrow\) x = -1; y = \(\dfrac{-1}{2}\)
Vậy ...
C = -12 - 3|x + 1| - 2(y - 1)2
Ta có: -3|x + 1| \(\le\) 0 với mọi x
-2(y - 1)2 \(\le\) 0 với mọi y
\(\Rightarrow\) -12 - 3|x + 1| - 2(y - 1)2 \(\le\) -12 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x + 1 = 0; y - 1 = 0
\(\Rightarrow\) x = -1; y = 1
Vậy ...
Phần D đề ko rõ là \(\dfrac{5}{2x^2}-3\) hay \(\dfrac{5}{2}\)x2 - 3 nữa
F = \(\dfrac{-5}{3}\) - 2x2
Ta có: -2x2 \(\le\) 0 với mọi x
\(\Rightarrow\) \(\dfrac{-5}{3}-2x^2\) \(\le\) \(\dfrac{-5}{3}\) với mọi x
Dấu "=" xảy ra khi và chỉ khi x = 0
Vậy ...
Chúc bn học tốt!
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của
-x^+3x+2
x(1-2x)
-x^-2y^+2xy-y+1
-x^2+3x+2
\(=-\left(x^2-3x-2\right)\)
\(=-\left(x^2-3x+\frac{9}{4}-\frac{17}{4}\right)\)
\(=-\left[\left(x-\frac{3}{2}\right)^2-\frac{17}{4}\right]\)
\(=-\left(x-\frac{3}{2}\right)^2+\frac{17}{4}\le\frac{17}{4}\)
=>GTLN khi \(x-\frac{3}{2}=0\)
\(\Rightarrow x=\frac{3}{2}\)
Đúng 0
Bình luận (0)
\(-x^2+3x+2=-\left(x^2-3x+\frac{9}{4}\right)+\frac{17}{4}=-\left(x-\frac{3}{2}\right)^2+\frac{17}{4}\le\frac{17}{4}\)
\(x.\left(1-2x\right)=x-2x^2=-2x^2+x=-2\left(x^2-\frac{1}{2}x\right)=-2.\left(x^2-\frac{2.x.1}{4}+\frac{1}{16}\right)+\frac{1}{8}=-2.\left(x-\frac{1}{4}\right)^2+\frac{1}{8}\le\frac{1}{8}\)
tự vt dấu = xảy ra nha :))
Đúng 0
Bình luận (0)
a) Cho x+y=1. Tìm giá trị nhỏ nhất của biểu thức A= \(x^2+y^2+x^3+y^3\)
b) Cho x+y+z =3. Tìm giá trị lớn nhất của B= xy +yz +xz
c) Cho x+2y =3 . Tìm GTNN của C = \(x+2y^2\)
d) Cho \(3x^2+y^2+2xy+4=7x+3y\)
a/ giá trị nhỏ nhất của A là 2
b/ giá trị lớn nhất của B là 51
tớ chỉ có bài tham khảo trên mạng thôi bạn thông cảm
Ta có: x + y = 1
<=> (x + y)3 = 1
<=> x3 + y3 + 3xy(x + y) = 1
<=> x3 + y3 + 3xy = 1 (do x + y = 1)
<=> x3 + y3 = 1 - 3xy
Áp dụng BĐT Cô - si, ta có:
xy >= (x+y)24=14(x+y)24=14
<=> -3xy≥−34≥−34
Ta có x3 + y3 = 1 - 3xy ≥1−34=14≥1−34=14
Dấu "=" xảy ra khi x = y = 1212
Vậy GTNN của x3 + y3 là 1414khi x = y = 12
c/ GTNN của C là 5
d/ y = 12 , x = 12
Xem thêm câu trả lời