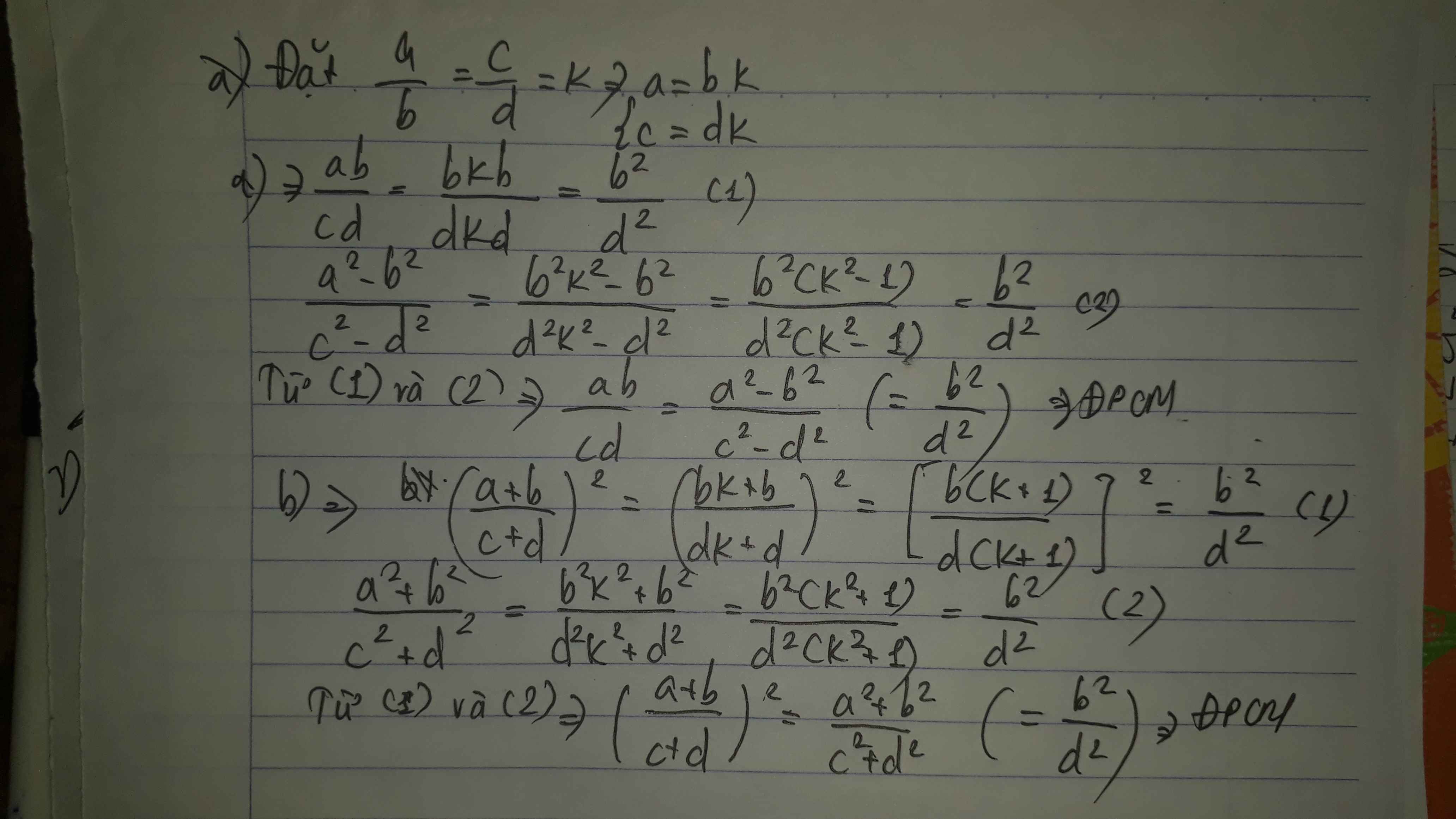cho tỉ lệ thức: a/b = c/d. chứng minh ta có tỉ lệ thức: a/b = a+c/b+d = a-c/b-d

Những câu hỏi liên quan
1.cho tỉ lệ thức a/b=c/d chứng minh rằng ta có tỉ lệ thức
a+b/b=c+d/d;a+b/a-b/c+d/c-d
Bài 7: Cho tỉ lệ thức dfrac{a}{b}dfrac{c}{d}. Chứng minh rằng ta có các tỉ lệ thức sau( giả thiết các tỉ lệ thức phải chứng minh đều có nghĩa):a)dfrac{a-b}{a+b}dfrac{c-d}{c+d} b)dfrac{2a+5b}{3a-4b}dfrac{2c+5d}{3c-4d}c)dfrac{ab}{cd}dfrac{left(a-bright)^2}{left(c-dright)^2} d)dfrac{ac}{bd}dfrac{a^2+c^2}{b^2+d^2}ai hộ mik vs
Đọc tiếp
Bài 7: Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh rằng ta có các tỉ lệ thức sau( giả thiết các tỉ lệ thức phải chứng minh đều có nghĩa):
a)\(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\) b)\(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
c)\(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\) d)\(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
ai hộ mik vs
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
Đúng 3
Bình luận (0)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
Đúng 2
Bình luận (0)
chứng minh rằng từ tỉ lệ thức a/b=c/d ta có thể suy ra tỉ lệ thức a+b/a-b=c+d/c-d
\(\frac{a}{b}=\frac{c}{d}\)\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)( 1 )
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
Đúng 1
Bình luận (0)
chứng minh. từ tỉ lệ thức a/b=c/d ta có thể suy ra tỉ lệ thức a+b/b=c+d/d
\(\frac{a}{b}=\frac{c}{d}\)\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{a+b}{b}=\frac{c+d}{d}\) (đpcm)
(Mik nghĩ zậy thui chứ ko chắc có trình bày đúng hay ko)
_Hok tốt_
!!!
Đúng 0
Bình luận (0)
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) . Chứng minh rằng ta có các tỉ lệ thức sau (giả thiết các tỉ lệ thức là có nghĩa ) :
a) \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b) \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
Chứng minh rằng từ tỉ lệ thức a/b = c/d ( a - b khác 0 , c - d khác 0 ) ta có thể suy ra tỉ lệ thức a+b/a-b = c + d/c-d
đặt x/2=y/5=k
=> x=2k, y=5k
ta có: 5kx2k=10
=> 10k^2=10
=> k^2=1
=> k=±1
với k=1=> x=2x1=2 ; y=1x5=5
với k=-1=> x=-1x2=-2 ; y=-1x5=-5
Đúng 0
Bình luận (0)
\(\frac{x}{2}=\frac{y}{5}\Rightarrow5x=2y\)(1)
=>5x-2y=0
=>-(2y-5x)=0
=>2y-5x=0 (1)
xy=10 (2)
=>ta có:\(\int^{2y-5x=0}_{xy=10}\)
giải ra ta đc:x=±2;y=±5
Đúng 0
Bình luận (0)
Chứng minh rằng từ tỉ lệ thức a/b=c/d (a - b khác 0, c - d khác 0 ) ta có thể suy ra tỉ lệ thức( a+b/a-b ) = (c+d / c- d )
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(đpcm)
Đúng 1
Bình luận (0)
ta có a/b , c/d suy ra AB=CD
và ta có : AD + AB = BC + AB
hoặc 1 cách nữa là : A . ( B+D ) = B ( A.C) (1)
và đề cho B và D khác ko => B+D không bằng 0
=> từ ( 1) ta có đc 1 tỉ lệ thức :
=> A/B = A+C phần B+D
Chứng minh rằng từ tỉ lệ thức a/b=c/d (a-b khác o,c-d khác o) ta có thể suy ra tỉ lệ thức a+b/a-b =c+d/c-d
\(\frac{a}{b}=\frac{c}{d}=>\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
\(=>\frac{a+b}{a-b}=\frac{c+d}{c-d}\left(\text{Đ}PCM\right)\)
Đúng 0
Bình luận (0)
Ta có : a/b = c/d => a/c = b/d
Áp dụng tính chất dãy tính chất tỉ số bằng nhau :
a/c = b/d = a+b/c+d = a-b/c-d => a+b/a-b = c+d/c-d
Đúng 0
Bình luận (0)
Chứng minh rằng từ tỉ lệ thức: a/b=c/d ( a-b khác 0, c-d khác 0) ta có thể suy ra tỉ lệ thức: a+b/a-b=c+d/c-d
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
\(\Rightarrow\left(a+b\right)\left(c-d\right)=\left(a-b\right)\left(c+d\right)\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(điều phải chứng minh)
Đúng 0
Bình luận (0)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
Đúng 0
Bình luận (0)