Câu 3 )
a) 2sinx + 2cosx -√2 = 0
b) 3sin3x - 4cos3x = 5
Giải các phương trình sau: a) cosx – √3sinx = √2; b) 3sin3x – 4cos3x = 5; c) 2sin2x + 2cos2x – √2 = 0; d) 5cos2x + 12sin2x -13 = 0.
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).
Giải phương trình sau: 3sin3x - 4cos3x = 5
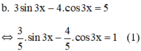
Ta có: 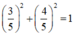 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 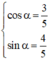
(1) trở thành: cos α.sin3x – sin α.cos 3x = 1
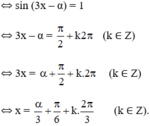
Vậy phương trình có họ nghiệm 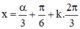 (k ∈ Z)
(k ∈ Z)
với α thỏa mãn 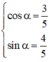
Giá trị lớn nhất của hàm số y = 3sin3x-4cos3x+5 ?
A. 5
B.10
C.4
D.12
Đáp án B
3sin3x - 4cos3x ≤ 3 2 + ( - 4 ) 2 = 5 => Maxy 5 + 5 =10
Giá trị lớn nhất của hàm số y = 3sin3x - 4cos3x + 5 ?
A. 5
B. 10
C. 4
D. 12
Đáp án B
Ta có: 3 sin 3 x - 4 cos 3 x ≤ 3 2 + - 4 2 = 5 ⇒ M a x R y = 5 + 5 = 10 .
1.2cos2x+2cosx-√2=0
2.cos6x+3sin3x+4=0
1.
\(2\left(2cos^2x-1\right)+2cosx-\sqrt{2}=0\)
\(\Leftrightarrow4cos^2x+2cosx-2-\sqrt{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{\sqrt{2}}{2}\\cosx=\frac{-1-\sqrt{2}}{2}< -1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm\frac{\pi}{4}+k2\pi\)
Tìm giá trị lớn nhất của hàm số y = 2 - 3 sin 3 x + 4 cos 3 x trên R.
A. m a x R y = 7
B. m a x R y = 5
C. m a x R y = 9
D. m a x R y = 3
Tìm giá trị lớn nhất của hàm số y=2-3sin3x+4cos3x trên R
A.![]()
B. ![]()
C. ![]()
D. ![]()
Phương trình: 3sin3x+ 3 cos9x= 2cosx+4 sin 3 3 x có số nghiệm trên 0 ; π 2 là
A. 2
B. 3
C. 4
D. lớn hơn hoặc bằng 5 nghiệm
Chọn D
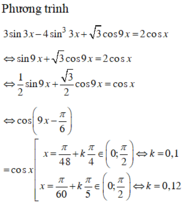
Vậy phương trình có 5 nghiệm thỏa mãn.
1) Gia tri lon nhat cua ham so: y = \(\dfrac{cosx+2sinx+3}{2cosx-sinx+4}\)
A. 0 B. 3-2\(\sqrt{3}\) C. \(2-2\sqrt{2}\) D. -1