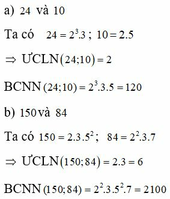Câu 3: a) Tìm ƯCLN(150;84)và BCNN(15;35;200).
b) Tìm tất cả các số tự nhiên n để 3n+13 chia hết cho n+1.

Những câu hỏi liên quan
Câu 1 :
a ) Tìm ƯCLN : ( a : b ) = 8
b ) a + b = 24 ; a < b
Câu 2 :
a ) Tìm ƯCLN : ( n + 1 ; 2n + 1 )
b ) Tìm ƯCLN : ( 2n + 1 ; 2n + 3 )
giúp ml với mk đang cần gấp !!!!!!!!!
cho a=22.32.39; b=65.24
a, tìm ƯCLN (a;b)
b,Tìm n\(\notin\)N biết 150<n<200, ƯCLN(6n+5;a)#1
tìm a,b thuộc n:
1)a+b=150 và ƯCLN(a,b)=5
2)a.b=768 VÀ ƯCLN(a,b)=8
1) Ta có:
a + b =150
ƯCLN (a, b) = 5
\(\Rightarrow\) a = 5.m trong đó ƯCLN(m, n) = 1 (vì ƯCLN(a,b) = 5)
b = 5.n
\(\Rightarrow\) 5m + 5n = 150
5 (m + n) = 150
\(\Rightarrow\) m + n = \(\frac{150}{5}\) = 30
| m | 29 | 23 | 21 | 19 | 17 |
| n | 1 | 7 | 9 | 11 | 13 |
| a= 5m | 145 | 115 | 105 | 95 | 85 |
| b= 5n | 5 | 35 | 45 | 55 | 65 |
Vậy a có thể bằng 145, 115, 105, 95, 85
b có thể bằng 5, 35, 45, 55, 65
Đúng 0
Bình luận (0)
2) Ta có:
a . b = 768
ƯCLN(a, b) = 8
\(\Rightarrow\) a = 8 . m trong đó ƯCLN(m; n) = 1 (vì ƯCLN(a,b) = 8)
b = 8 . n
\(\Rightarrow\) 8m . 8n = 768
\(\Rightarrow\) m . n = \(\frac{768}{8^2}\)= 12
| m | 12 | 4 |
| n | 1 | 3 |
| a = 8m | 96 | 32 |
| b = 8n | 8 | 24 |
Vậy a bằng 96 và b bằng 8
a bằng 32 và b bằng 24
Đúng 0
Bình luận (0)
Câu 3. Tìm ƯCLN(100; 120)
Trả lời:
100 = …………
120 = ………….
ƯCLN(100; 120) = ……………………
Lời giải:
$100=2^2.5^2$
$120=2^3.3.5$
$\Rightarrow ƯCLN(100,120)=2^2.5=20$
Đúng 1
Bình luận (0)
Tìm ƯCLN(126, 150), sau đó tìm tất cả ƯC nhờ ƯCLN của hai số đó.
126 = 2.32.71
50 = 2.3.52
ƯCLN(126, 150) = 2.3 = 6
ƯC(126, 150) = {1,2,3,6}.
Đúng 0
Bình luận (0)
Tìm số tự nhiên a, biết a×b=150 và ƯCLN(a,b)=5
hãy tìm ƯCLN(150 và 1000) rồi tìm ƯC(150 và 1000)
\(150=5^2\cdot2\cdot3;1000=2^3\cdot5^3\)
=>\(ƯCLN\left(150;1000\right)=5^2\cdot2=50\)
=>\(ƯC\left(150;1000\right)=Ư\left(50\right)=\left\{1;-1;2;-2;5;-5;10;-10;25;-25;50;-50\right\}\)
Đúng 0
Bình luận (1)
Ta có:
150=2.3.52
1000=23.52.7
=>ƯCLN(150;1000)=2.5=10
=>ƯC(150;1000)={1;2;5;10}
Đúng 0
Bình luận (0)
Ta có:
150=2.3.52
1000=23.52.7
=>ƯCLN(150;1000)=2.5=10
=>ƯC(150;1000)={-1;-2;-5;-10;1;2;5;10}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm ƯCLN và BCNN của:
a) 24 và 10
b) 150 và 84
Tìm ƯCLN(126, 150), sau đó tìm tất cả ƯC nhờ ƯCLN của hai số đó.
\(126=2.3^2.7\)
\(150=2.3.5^2\)
Các thừa số nguyên tố chung của 126 và 150 là 2 và 3
Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.
Do đó: \(ƯCLN\left(126;150\right)=21.31=2.3=6\)
Lại có 6 có các ước là \(1;2;3;6\)
Ước chung của 126 và 150 là ước của \(ƯCLN\left(126;150\right)=1;2;3;6\)
Hay \(ƯC\left(126;150\right)=\left\{1;2;3;6\right\}\)
Vậy \(ƯCLN\left(126;150\right)=6;ƯC\left(126;150\right)=\left\{1;2;3;6\right\}\)

Do đó: 126 = 2 . 3 . 3 . 7 = 2 . 32 . 7
150 = 2 . 3 . 5 . 5 = 2 . 3 . 52
Các thừa số nguyên tố chung của 126 và 150 là 2 và 3
Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.
Do đó: ƯCLN(126, 150) = 21 . 31 = 2 . 3 = 6
Lại có 6 có các ước là 1; 2; 3; 6
Ước chung của 126 và 150 là ước của ƯCLN(126, 150) là 1; 2; 3; 6
Hay ƯC(126, 150) = {1; 2; 3; 6}
Vậy ƯCLN(126, 150) = 6; ƯC(126, 150) = {1; 2; 3; 6}.
trả lời :
Ư(126) = { 1; 126; 63; 2; 3; 42; 6; 21; 7; 18; 9; 14 }
ƯC = { 1; 2; 3; 18; 6; 9 }
ƯCLN : 18
Ư(150) = { 1; 150; 2; 75; 50; 3; 5; 30; 6; 25 15; 10}
ƯC = { 1; 2; 3; 30; 15; 10; 6; 5 }
ƯCLN : 30
^HT^
Câu : Tìm 2 số tự nhiên biết tổng ƯCLN và BCNN của chúng bằng 23
Câu 2: Tìm \(x\in N\) biết: 2+4+6+...+2x= 156
Bài 1:
Gọi 2 số là $a$ và $b$.
$23=BCNN(a,b)+ƯCLN(a,b)\vdots ƯCLN(a,b)$
$\Rightarrow ƯCLN(a,b)=1$ hoặc $ƯCLN(a,b)=23$
Hiển nhiên nếu $ƯCLN(a,b)=23$ thì $BCNN(a,b)=0$
$\Rightarrow BCNN(a,b)< ƯCLN(a,b)$ (loại)
$\Rightarrow ƯCLN(a,b)=1$
$\Rightarrow BCNN(a,b)=22$
Khi $a,b$ nguyên tố cùng nhau thì $BCNN(a,b)=22=ab$
$\Rightarrow (a,b)=(1,22), (2,11), (11,2), (22,1)$
Đúng 0
Bình luận (0)
Bài 2:
$2+4+6+....+2x=156$
Số số hạng: $(2x-2):2+1=x$
Suy ra: $2+4+6+....+2x=(2x+2)x:2=x(x+1)=156=12.13$
$\Rightarrow x=12$
Đúng 0
Bình luận (0)