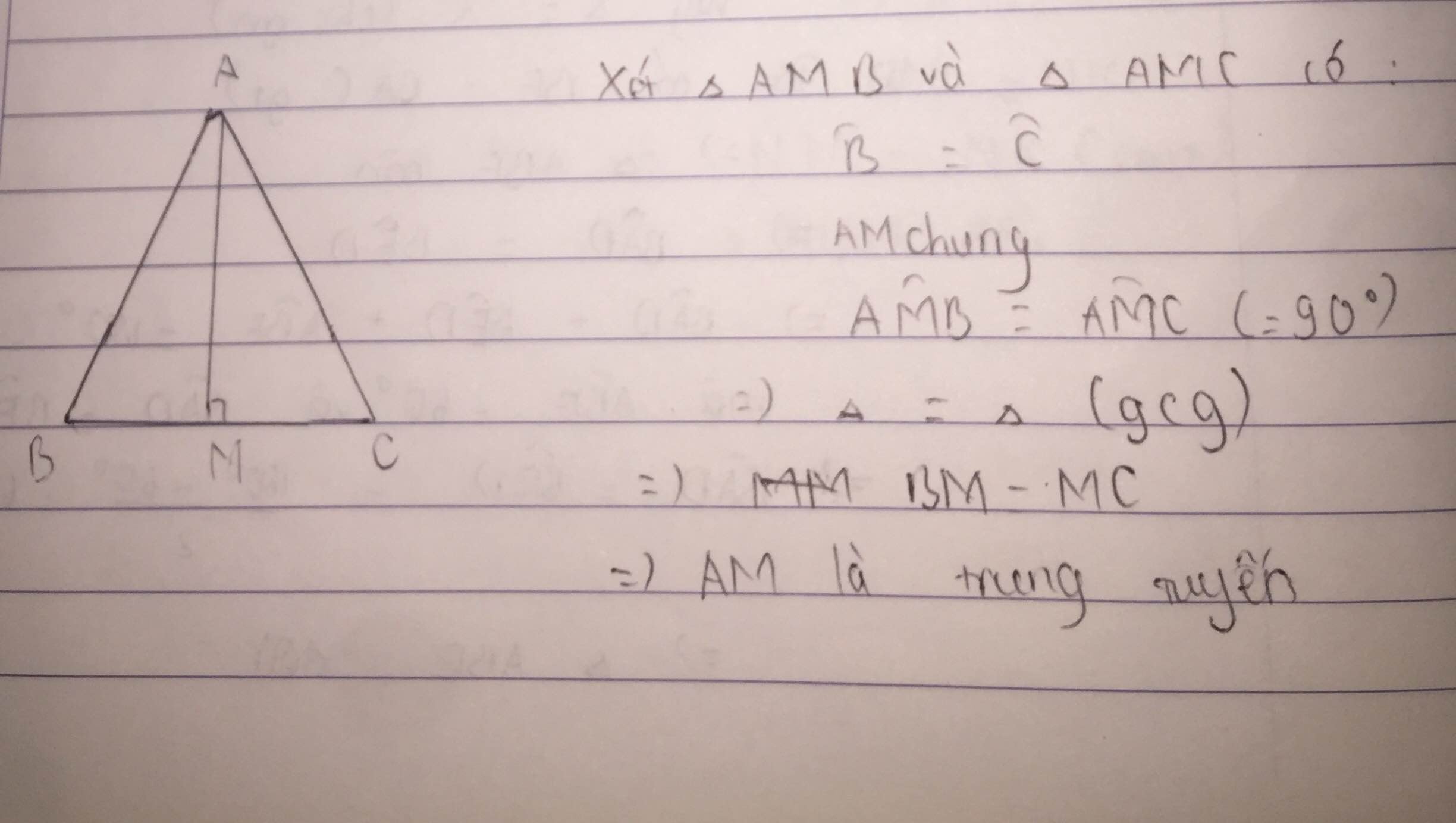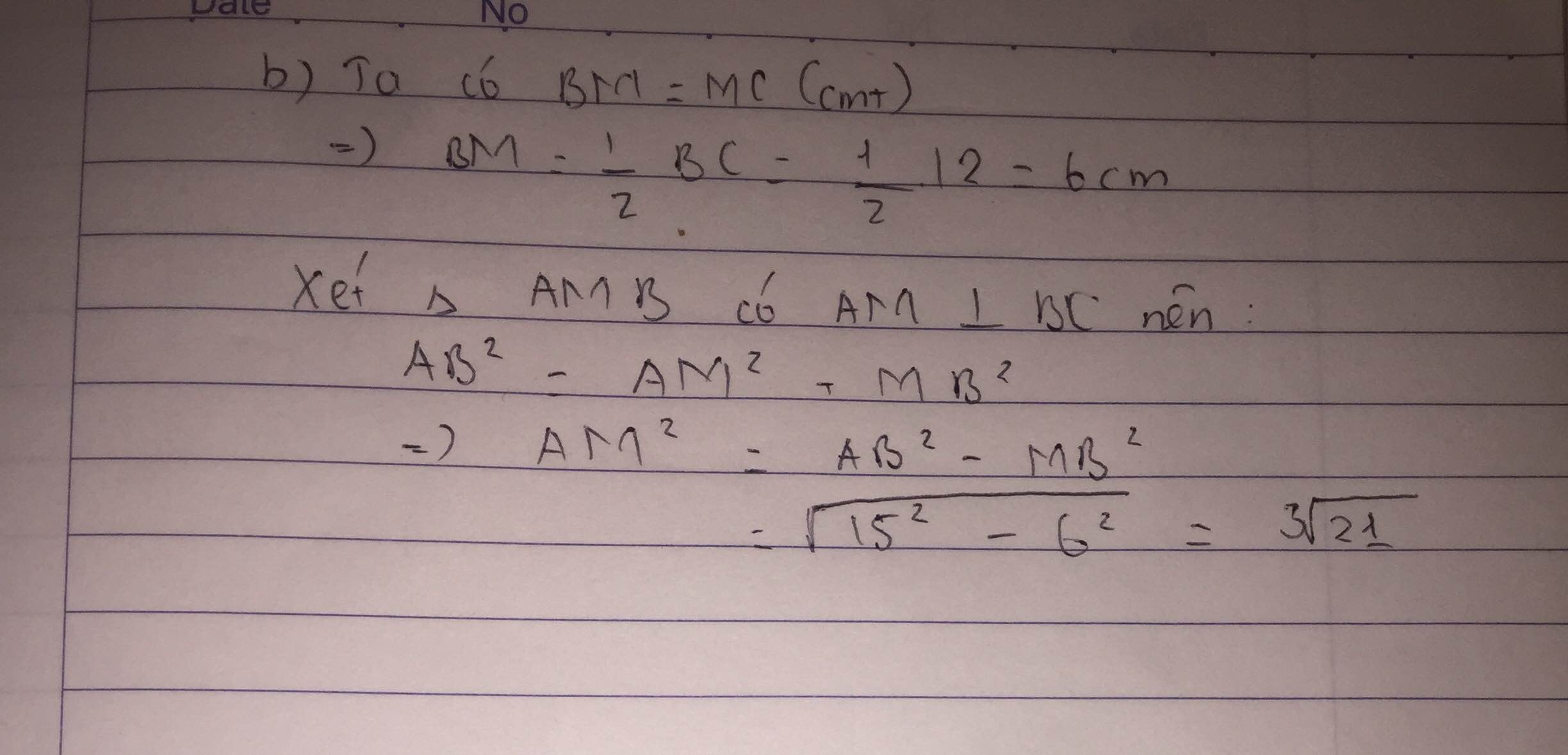Câu 1: Cho △ABC có đường trung tuyến AM thỏa mãn: BC=2.AM. CM: △ABC vuông tại A

Những câu hỏi liên quan
Câu 1. Tính: Cho tam giác ABC vuông tại A có AB = 9 cm BC = 15 cm . Đường cao AH, trung tuyến AM. Tỉnh AC, AH, BH, AM và diện tích tam giác AHM
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=7,5\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\\BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)
Áp dụng PTG: \(HM=\sqrt{AM^2-AH^2}=2,1\left(cm\right)\)
Vậy \(S_{AHM}=\dfrac{1}{2}HM\cdot AH=\dfrac{1}{2}\cdot2,1\cdot7,2=7,56\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc vuông tại a có đường trung tuyến am biết bc = 101 cm tính cho độ dài am
Bài 1. Cho tam giác ABC cân tại A. Kẻ AM vuông góc với BC tại M
a) Chứng minh AM là trung tuyến của tam giác
b) Biết AB = 15 cm; BC = 12 cm. Tính độ dài đường trung tuyến AM.
cho tam giác ABC có trung tuyến AM sao cho AM = 1/2 BC . cm rằng tam giác ABC vuông tại A
\(AM=\frac{1}{2}BC=BM=CM\)
suy ra \(\Delta AMB,\Delta AMC\)đều cân tại \(M\).
suy ra \(\widehat{MAB}=\widehat{MBA},\widehat{MCA}=\widehat{MAC}\)
\(\Rightarrow\widehat{ABC}=\widehat{MAB}+\widehat{MAC}=\widehat{MBA}+\widehat{MCA}=\widehat{CBA}+\widehat{BCA}\)
\(\Rightarrow\widehat{ABC}=\frac{180^o}{2}=90^o\)
Ta có đpcm.
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
cho tam giác ABC vuông tại A . có đg trung tuyến AM
cm AM =1/2 BC
ta có mc=mb(gt)
có tam giác abc(góc a =90)
=)am = 1/2bc(tính chất đường trung tuyến trong tam giác vuông).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AM là trung tuyến, cm AM= 1/2 BC
Ta có BM=CM ( AM là đg trung tuyến )
Xét tam giác ABC có
Góc A=90’
=>AM=1/2 BC ( t/c đg trung tuyến trong một tam giác vuông)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AM là trung tuyến.
A) CM: AM=1/2 BC
B) Nếu AM=1/2 BC thì tam giác ABC vuô g tại A
cho tam giác abc vuông tại a có ab=20cm, bc = 25 cm. ba đường trung tuyến am, bn, ce cắt nhau tại O. tính độ dài am. bn, ce
\(BC^2=AB^2+AC^2\left(Pitago\right)\)
\(\Rightarrow AC^2=BC^2-AB^2=625-400=225\)
\(\Rightarrow AC=15\left(cm\right)\)
\(AM^2=\dfrac{2.\left(AB^2+AC^2\right)-BC^2}{4}\) (Độ dài trung tuyến trong tam giác)
\(\Rightarrow AM^2=\dfrac{2.\left(400+225\right)-625}{4}=\dfrac{625}{4}\)
\(\Rightarrow AM=\dfrac{25}{2}\left(cm\right)=12,5\left(cm\right)\)
Tương tự ...
\(BN^2=\dfrac{2.\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Rightarrow BN^2=\dfrac{2.\left(400+625\right)-225}{4}=\dfrac{1825}{4}\)
\(\Rightarrow BN=\sqrt[]{\dfrac{1825}{4}}=\sqrt[]{\dfrac{73.25}{4}}=\dfrac{5\sqrt[]{73}}{4}\left(cm\right)\)
\(CE^2=\dfrac{2.\left(AC^2+BC^2\right)-AB^2}{4}\)
\(\Rightarrow CE^2=\dfrac{2.\left(225+625\right)-400}{4}=\dfrac{1300}{4}\)
\(\Rightarrow CE=\sqrt[]{\dfrac{1300}{4}}=\sqrt[]{\dfrac{13.100}{4}}=\dfrac{10\sqrt[]{13}}{4}=\dfrac{5\sqrt[]{13}}{2}\left(cm\right)\)
Đúng 1
Bình luận (0)
Đính chính
\(BN=\dfrac{5\sqrt[]{73}}{2}\left(cm\right)\)
\(CE=\dfrac{10\sqrt[]{13}}{2}=5\sqrt[]{13}\left(cm\right)\)
Đúng 1
Bình luận (0)