Giả sử hội trường có a dãy và b là số ghế của mỗi dãy. (a,b∈N∗a,b∈N∗).

Ta có phương trình: ab=500ab=500 và 

⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25

Vậy lúc đầu người ta định xếp 2525 dãy ghế.

Gọi số dãy ghế là x>2 và số người một dãy ghế là y>1

\(\Rightarrow\) Số người dự định: \(xy\)

Khi bớt 2 dãy ghế và mỗi ghế thêm 1 người thì số người ngồi: \(\left(x-2\right)\left(y+1\right)\)

Khi thêm 3 dãy ghế và mỗi dãy ghế bớt 1 người thì số người: \(\left(x+3\right)\left(y-1\right)\)

Theo bài ra ta có hệ: \(\left\{{}\begin{matrix}\left(x-2\right)\left(y+1\right)=xy+8\\\left(x+3\right)\left(y-1\right)=xy-8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=10\\-x+3y=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=20\\y=5\end{matrix}\right.\)

Vậy có 20 dãy ghế

Gọi số dãy ghế trong hội trường là x (x nguyên dương)

Số ghế của mỗi dãy ghế lúc đầu là 150/x

Số dãy ghế lúc sau là x + 2

Số ghế của mỗi dãy ghế lúc sau là

Đáp án: D

Gọi số dãy ghế ban đầu của hội trường là a (dãy), số chỗ ở mỗi dãy ban đầu ở hội trường là b (chỗ)

Nếu bớt 2 dãy ghế và mỗi dãy thêm 1 chỗ thì thêm được 8 chỗ: \(\left(a-2\right)\left(b+1\right)=ab+8\Leftrightarrow ab+a-2b-2=ab+8\Leftrightarrow a-2b-10=0\left(1\right)\)

Nếu thêm 3 dãy ghế và mỗi dãy ghế bớt đi 1 chỗ thì giảm 8 chỗ:

\(\left(a+3\right)\left(b-1\right)=ab-8\Leftrightarrow ab-a+3b-3=ab-8\Leftrightarrow-a+3b+5=0\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}a-2b=10\\-a+3b=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=20\\b=5\end{matrix}\right.\)

Vậy số dãy ghế ban đầu của hội trường là 20 dãy

Gọi số dãy ghế trong phòng họp là x (dãy) (x thuộc N*, x > 3)
Vì trong phòng có 360 người nên mỗi dãy có số người là 360:x
Nếu bớt đi 3 dãy và thêm vào mooic dãy 4 người thì số người vẫn không thay đổi nên ta có phương trình :
                         (x -3)(360:x +4) = 360 
                  <=>  360 + 4x -1080:x -12 = 360
                  <=>  4x^2-12x -1080 =0
                  <=>   x^2 - 3 x -270 =0
                  <=>   x^2 - 18x +15x -270 =0
                  <=>   (x -18)(x +15) = 0
                  <=>   x= 18 (thỏa mãn) hoặc x=-15 (loại)
 Vậy số dãy trong phòng họp là 18 dãy
 ĐÚNG HỘ NHA!!!!

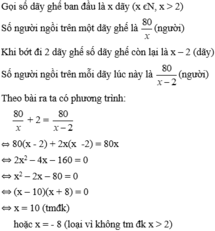
Vậy số dãy ghế ban đầu là 10 dãy và số người ngồi trên 1 dãy là 8 người.

bài mẫu nè:

gọi số dãy ghế là x, số ghê là y 
theo đb ta có hpt 
(x-2)(y+2)=288 
xy=288 
giải pt tìm đk x=18; y=16 

Gọi x là số dãy ghế; y là số người trên mỗi dãy ghế (x,y>0) 
Ta có tổng cộng 80 người nên x*y =80 <=> x =80/y (1) 
Nếu bớt đi 2 dãy ghế tức x-2 thì mỗi dãy còn lại phải xếp thêm 2 người tức y+2 
Ta có: (x-2)*(y+2) = 80 (2) 
Thay (1) vào (2) ta có: 2y^2 +4y -160 =0 
<=> y=8 => x=10 
Vậy có 10 dãy ghế và có 8 người trên mỗi dãy

Gọi x là số dãy ghế trong phòng họp ( x nguyên ; x>2)

Số người ngồi trên 1 dãy là \(\frac{80}{x}\)(người)

Nếu bới đi 2 dãy thì số dãy ghế còn lại là : x - 2 (dãy)

Số người ngồi trên mỗi dãy sẽ là: \(\frac{80}{x-2}\)(người )

Ta có phương trình :

\(\frac{80}{x-2}-\frac{80}{x}=2\Leftrightarrow\frac{40}{x-2}-\frac{40}{x}=1\Leftrightarrow x^2-2x-80=0\)

Giaỉ phương trình ta được \(x_1=10;x_2=-8\left(lọai\right)\)

Vậy số dãy ghế lúc đầu là 10 dãy và mỗi dãy xếp 8 người ngồi

MÌNH GIẢI SAI MONG CÁC BẠN THÔNG CẢM VÀ SỬA JUP MIK!!

Gọi số dãy ghế lúc đầu là x (dãy ghế) Đk: x>2

          Số ghế mỗi dãy lúc đầu là 210/x(ghế) 

          dãy ghế lúc sau là x+2(dãy ghế)

          Số ghế mỗi dãy lúc sau là 272/x+2(ghế)

Vì thực tế phải xếp thêm mỗi dãy 2 ghế nên ta có pt:

(210/x)-(272/x+2)+2=0(1)

Giải pt (1) ta có: x₁=15(TM),x₂=14(TM)

Với số dãy ghế lúc đầu là 15 (dãy) suy ra mỗi dãy có số ghế là 14 (ghế)

Với số dãy ghế lúc đầu là 14 (dãy) suy ra mỗi dãy có số ghế là 15 (ghế)