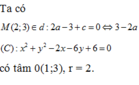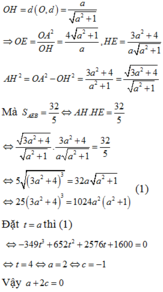Cho đường tròn (C): x2+y2+2x-6y+2=0 và điểm M(-2;1). Đường thẳng (d) qua M và cắt đường tròn tạo 2 điểm A, B thỏa mãn M là trung điểm AB có phương trình là:

Những câu hỏi liên quan
Cho đường tròn (C) có phương trình
x
2
+
y
2
+
2
x
−
6
y
+
2
0
và điểm M(-2; 1). Đường thẳng ∆ qua M(-2; 1) cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là: A.x + y + 1 0 B.x – y + 3 0 C.2x – y + 5 0 D.x + 2y 0
Đọc tiếp
Cho đường tròn (C) có phương trình x 2 + y 2 + 2 x − 6 y + 2 = 0 và điểm M(-2; 1). Đường thẳng ∆ qua M(-2; 1) cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là:
A.x + y + 1 = 0
B.x – y + 3 = 0
C.2x – y + 5 = 0
D.x + 2y = 0
ĐÁP ÁN D
Đường tròn (C) có tâm I( -1; 3).
Do đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB nên I M ⊥ Δ ( quan hệ vuông góc đường kính và dây cung).
Đường thẳng ∆: đi qua M(-2; 1) và nhận M I → ( 1 ; 2 ) làm VTPT nên có phương trình là :
1. (x + 2) + 2(y – 1) = 0 hay x+ 2y = 0
Đúng 0
Bình luận (0)
Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y - 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 - 4x + 6y – 3 = 0
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính 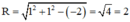
b) 16x2 + 16y2 + 16x – 8y –11 = 0
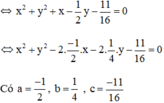
⇒ Đường tròn có tâm 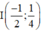 , bán kính
, bán kính 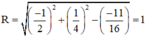
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính 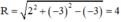
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
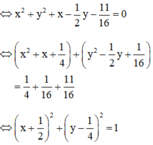
Vậy đường tròn có tâm 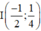 và bán kính R = 1.
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
Đúng 0
Bình luận (0)
Cho đường tròn (C): x 2 + y 2 + 2x + 2y - 2 = 0 và điểm M(-1;1). Phương trình tiếp tuyến của đường tròn tại M là:
A. y - 1 = 0
B. y + 1 = 0
C. x - 1 = 0
D. x + 1 = 0
Đáp án: A
Ta có:
(C): x 2 + y 2 + 2x + 2y - 2 = 0 ⇔ (x + 1 ) 2 + (y + 1 ) 2 = 4 ⇒ I(-1;-1)
Phương trình tiếp tuyến của đường tròn tại M là đường thẳng đi qua M và nhận vector IM = (0;2) làm vecto pháp tuyến: 0.(x + 1) + 2.(y - 1) = 0 ⇔ y - 1 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 0 và đường tròn (C) có phương trình:
x
2
+
y
2
+
2
x
−
6
y
+
6
0
.Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đườn...
Đọc tiếp
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 = 0 và đường tròn (C) có phương trình: x 2 + y 2 + 2 x − 6 y + 6 = 0 .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .
Đúng 0
Bình luận (0)
Đường tròn (C): x2+y2-2x-6y=0. Tìm tọa độ M thuộc đường thẳng x=3 để từ M kẻ được tới (C) 2 tiếp tuyến vuông góc.
Đường tròn (C) tâm \(I\left(1;3\right)\) bán kính \(R=\sqrt{10}\)
Gọi 2 tiếp điểm là A và B \(\Rightarrow\) tứ giác IAMB là hình chữ nhật (có 3 góc vuông)
Mà \(IA=IB=R\Rightarrow IAMB\) là hình vuông (hcn có 2 cạnh kề bằng nhau)
\(\Rightarrow IM=IA\sqrt{2}=R\sqrt{2}=2\sqrt{5}\)
Gọi \(M\left(3;m\right)\Rightarrow\overrightarrow{IM}=\left(2;m-3\right)\)
\(\Rightarrow IM=\sqrt{4+\left(m-3\right)^2}=2\sqrt{5}\)
\(\Leftrightarrow\left(m-3\right)^2=16\Rightarrow\left[{}\begin{matrix}m=-1\\m=7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(3;-1\right)\\M\left(3;7\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
x
2
+
y
2
-
8
x
+
6
y
+
21
0
và đường thẳng d: 2x+y-30. Đường tròn (C) nội tiếp hình vuông ABCD. Tìm tọa độ điểm A, biết rằng điểm A nằm trên đường thẳng d và hoành độ điểm A nguyên A. A(2;-1) B. A(-2;7) C. A(1;1) D. A(-1;5)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x 2 + y 2 - 8 x + 6 y + 21 = 0 và đường thẳng d: 2x+y-3=0. Đường tròn (C) nội tiếp hình vuông ABCD. Tìm tọa độ điểm A, biết rằng điểm A nằm trên đường thẳng d và hoành độ điểm A nguyên
A. A(2;-1)
B. A(-2;7)
C. A(1;1)
D. A(-1;5)
Cho đường tròn (C):
x
2
+
y
2
- 2x + 6y + 8 0 và đường thẳng d: x + y + 4 0. Phương trình tiếp tuyến của đường tròn (C) và song song với đường thẳng d là: A.
x
+
y
-
4
0
B.
[
x
+
y
0...
Đọc tiếp
Cho đường tròn (C): x 2 + y 2 - 2x + 6y + 8 = 0 và đường thẳng d: x + y + 4 = 0. Phương trình tiếp tuyến của đường tròn (C) và song song với đường thẳng d là:
A. x + y - 4 = 0
B. [ x + y = 0 x + y + 4 = 0
C. x + y = 0
D. x + y - 2 = 0
Đáp án: B
(C): x 2 + y 2 - 2x + 6y + 8 = 0
⇔ (x - 1 ) 2 + (y + 3 ) 2 = 2 có I(1;-3), R = 2
Gọi d’ là tiếp tuyến của đường tròn (C) và song song với d
Vì d'//d ⇒ d': x + y + c = 0, (c ≠ 4)
d’ là tiếp tuyến của (C) nên d(I;d') = R
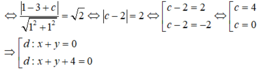
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường tròn (C) : x2 + y2+ -4x-6y-120 Gọi M là điểm trên d: 2x-y+30 sao cho MI 2R sao cho MI 2R với I, R lần lượt là tâm và bán kính của (C). Tổng hoành độ các điểm M thỏa mãn là A.1/4 B. 4/5 C. -1/5 D. -4/5
Đọc tiếp
Trong mặt phẳng Oxy, cho đường tròn (C) : x2 + y2+ -4x-6y-12=0 Gọi M là điểm trên d: 2x-y+3=0 sao cho MI = 2R sao cho MI = 2R với I, R lần lượt là tâm và bán kính của (C). Tổng hoành độ các điểm M thỏa mãn là
A.1/4
B. 4/5
C. -1/5
D. -4/5
a)Viết phương trình đường tròn đi qua 3 điểm A(-1;1);B(3;1);C(1;3)
b)Cho (C):x2+y2-4x+6y+3=0 và (Δ):3x-y+m=0.Tìm m để đường thẳng (Δ) tiếp xúc với đường tròn (C)
a) Gọi đường tròn cần tìm là \(\left(C\right):x^2+y^2-2ax-2by+c=0\)
\(A\left(-1;1\right)\in\left(C\right)\Rightarrow1+1+2a-2b+c=0\Rightarrow2a-2b+c=-2\)
\(B\left(3;1\right)\in\left(C\right)\Rightarrow9+1-6a-2b+c=0\Rightarrow-6a-2b+c=-10\)
\(C\left(1;3\right)\in\left(C\right)\Rightarrow1+9-2a-6b+c=0\Rightarrow-2a-6b+c=-10\)
Giải hệ phương trình ta được: \(a=1;b=1;c=-2\)
Vậy đường tròn cần tìm là: \(x^2+y^2-2x-2y-2=0\)
Đúng 0
Bình luận (0)
b) Ta có \(\left(C\right):x^2+y^2-4x+6y+3=0\)
\(\Rightarrow a=\dfrac{-4}{-2}=2;b=\dfrac{6}{-2}=-3;c=3\)
\(\Rightarrow I\left(2;-3\right)\) là tâm, bán kính \(R=\sqrt{2^2+\left(-3\right)^2-3}=\sqrt{10}\)
Để \(\left(\Delta\right)\) tiếp xúc đường tròn \(\Leftrightarrow d\left(I;\Delta\right)=R\)
\(\Leftrightarrow\dfrac{\left|9+m\right|}{\sqrt{10}}=\sqrt{10}\Leftrightarrow\left|9+m\right|=10\Leftrightarrow\left[{}\begin{matrix}9+m=10\\9+m=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-19\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường tròn (C):
x
2
+
y
2
-
2
x
-
6
y
+
6
0
. Đường thẳng (d) đi qua M(2;3) cắt (C) tại hai điểm A, B. Tiếp tuyến của đường tròn tại A và cắt nhau tại E. Biết
S
A
E
B
32
5...
Đọc tiếp
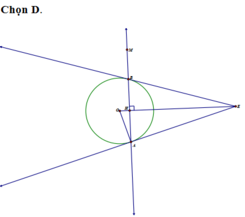
Trong mặt phẳng Oxy, cho đường tròn (C): x 2 + y 2 - 2 x - 6 y + 6 = 0 . Đường thẳng (d) đi qua M(2;3) cắt (C) tại hai điểm A, B. Tiếp tuyến của đường tròn tại A và cắt nhau tại E. Biết S A E B = 32 5 và phương trình đường thẳng (d) có dạng a x - y + c = 0 với a , c ∈ ℤ , a > 0 . Khi đó a + 2 c bằng:
A. 1
B. -1
C. -4
D. 0