cho tam giác ABC có góc A =hai lần góc B chứng minh rằng a2-b2= bc

Những câu hỏi liên quan
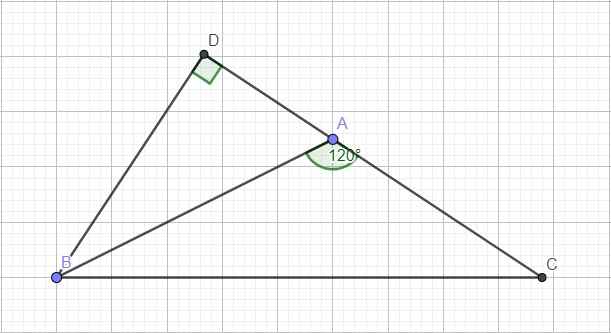
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
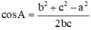
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Đúng 0
Bình luận (0)
Bài 4.Cho V ABC cân tại A có góc A 40 độ.Trên cạnh AB lấy điểm D,trên tia đối của tia CA lấy điểm E sao cho BD CE. Kẻ DH và EK cùng vuông góc với đường thẳng BC. (H,K thuộc BC).1) Tính góc B, gócC của tam giác ABC.2)Chứng minh DHEK.3)Gọi M là trung điểm của HK,chứng minh M là trung điểm của DE.Bài 5.Chứng minh rằng nếu a/bb/c thì a2+b2/b2+c2 a/c với b,c khác 0.
Đọc tiếp
Bài 4.Cho V ABC cân tại A có góc A =40 độ.Trên cạnh AB lấy điểm D,trên tia đối của tia CA lấy điểm E sao cho BD= CE. Kẻ DH và EK cùng vuông góc với đường thẳng BC. (H,K thuộc BC).
1) Tính góc B, gócC của tam giác ABC.
2)Chứng minh DH=EK.
3)Gọi M là trung điểm của HK,chứng minh M là trung điểm của DE.
Bài 5.Chứng minh rằng nếu a/b=b/c thì a2+b2/b2+c2= a/c với b,c khác 0.
Cho tam giác ABC có Â = 2 B ^ . Đặt AB = a, AC = b, BC = a. Chứng minh a 2 = b 2 + b c .
Cho tam giác ABC có a 2 = b 2 + c 2 - b c . Số đo của góc A là
A. 135 °
B. 150 °
C. 60 °
D. 120 °
Ta có: a2 = b2 +c2 – bc nên b2 + c2 – a2 = bc
Áp dụng hệ quả định lí cosin trong tam giác ta có:
cos A = b 2 + c 2 − a 2 2. b c = b c 2 b c = 1 2 ⇒ A ^ = 60 °
Chọn C
Đúng 0
Bình luận (0)
Cho tam giác ABC có a2 = b2 + c2 − bc. Góc B bằng bao nhiêu?
A. 1500 B. 1200 C. 600 D. 300
1 Cho tam giác ABC và tam giác A'B'C' có góc A = góc A' BC = B'C' góc B = B' chứng minh rằng tam giác ABC = tam giác A'B'C'
2 Cho tam giác ABC có AB = AC phân giác AD chứng minh rằng AD vuông góc với BC
AI TRA LỜI NHANH GIÚP MÌNH VỚI TvT
2. \(\Delta ABC\)có AB=AC \(\Rightarrow\Delta ABC\)cân.
AD là phân giác \(\Delta ABC\)mà \(\Delta ABC\)cân.
\(\Rightarrow AD\)l là đường trung trực \(\Delta ABC\)..
\(\Rightarrow AD\)là đường cao \(\Delta ABC\)..
\(\Leftrightarrow AD\perp BC\).
Hình 1 :
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có : Góc A = Góc A' ( gt ); \(BC=B'C'\left(gt\right)\); Góc B = Góc B' ( gt )
\(\Rightarrow\Delta ABC=\Delta A'B'C\left(ch-gn\right)\)
Hình 2 :
Vì \(\Delta ABC\) có \(AB=AC\Leftrightarrow\Delta ABC\) cân tại A . Vì AD là phân giác góc A
\(\Leftrightarrow\) ^BAD = ^CAD. Xét \(\Delta ABD\) và \(\Delta ACD\) có : \(AB=AC\left(gt\right)\); ^BAD = ^CAD; AD chung.
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\Leftrightarrow\) ^ADB = ^ADC ( tương ứng ) . Mà ^ADB + ^ADC = 1800 ( kề bù )
\(\Leftrightarrow\) ^ADB = ^ADC = 1800 : 2 = 900 nên suy ra \(AD\perp BC\)
Xem thêm câu trả lời
b1 Cho tam giác ABC có AB = AC. Trên cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = AE. Chứng minh rằng góc ADE = góc ABC từ đó suy ra DE // BC.
b2 Cho tam giác ABC đều có ba cạnh bằng 6 cm. Lấy điểm M trên cạnh BC, điểm N trên cạnh AC sao cho MC = NC = 1 cm. Tính chu vi tứ giác ABMN.
B1: \(y=\frac{1}{x^2+\sqrt{x}}\)vì AB=AC=> tam giác ABC cân tại A=> góc B=góc C=> góc B=(180 độ-góc A)/2 (1)
Vì AD=AE=> tam giác ADE cân tại A=> góc ADE=góc AED=> góc ADE=(180 độ-góc A)/2 (2)
Từ (1) và (2)=> góc B=góc ADE
Mà góc B và góc ADE là hai góc đồng vị=> DE//BC
B2: Hình như là 17 cm. Hi hi
Đúng 0
Bình luận (0)
bỏ cái chỗ \(y=\frac{1}{x^2+\sqrt{x}}\) hộ mình cái. mk bấm nhầm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = a 5 ; BC = a 3 ; AC = a 2
a, Chứng minh tam giác ABC là tam giác vuông
b, Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A
Cho tam giác ABC có góc B = 2 lần góc C. Chứng minh rằng : AC2 = AB(AB + BC).