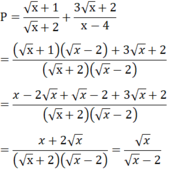`A=(x/[x^2-4]+2/[2-x]+1/[2+x]).[x+2]/2`

`a)ĐK: x \ne +-2`

`b)` Với `x \ne +-2` có:

`A=[x-2(x+2)+x-2]/[(x-2)(x+2)].[x+2]/2`

`A=[x-2x-4+x-2]/[x-2]. 1/2`

`A=[-3]/[x-2]`

`c)x=-1` t/m đk `=>` Thay `x=-1` vào `A` có: `A=[-3]/[-1-2]=1`

a/ Để rút gọn biểu thức A, chúng ta có thể thực hiện các bước sau:

Áp dụng các bước trên, ta có: A = (1/(2√x - 2)) + (1/(2√x + 2)) + (√x/(1 - x))

Bây giờ, chúng ta sẽ rút gọn biểu thức này: A = (1/(2√x - 2)) + (1/(2√x + 2)) + (√x/(1 - x)) = [(2√x + 2) + (2√x - 2) + (√x(2√x - 2)(2√x + 2))]/[(2√x - 2)(2√x + 2)(1 - x)] = [4√x + √x(4x - 4)]/[(4x - 4)(1 - x)] = [4√x + 4√x(x - 1)]/[-4(x - 1)(x - 1)] = [4√x(1 + x - 1)]/[-4(x - 1)(x - 1)] = -√x/(x - 1)

b/ Để tính giá trị của A với x = 4/9, ta thay x = 4/9 vào biểu thức đã rút gọn: A = -√(4/9)/(4/9 - 1) = -√(4/9)/(-5/9) = -√(4/9) * (-9/5) = -2/3 * (-9/5) = 6/5

Vậy, khi x = 4/9, giá trị của A là 6/5.

c/ Để tính giá trị của x sao cho giá trị tuyệt đối của A bằng 1/3, ta đặt: |A| = 1/3 |-√x/(x - 1)| = 1/3

Vì A là một số âm, ta có: -√x/(x - 1) = -1/3

Giải phương trình trên, ta có: √x = (x - 1)/3 x = ((x - 1)/3)^2 x = (x - 1)^2/9 9x = (x - 1)^2 9x = x^2 - 2x + 1 x^2 - 11x + 1 = 0

Sử dụng công thức giải phương trình bậc hai, ta có: x = (11 ± √(11^2 - 4 * 1 * 1))/2 x = (11 ± √(121 - 4))/2 x = (11 ± √117)/2

Vậy, giá trị của x để giá trị tuyệt đối của A bằng 1/3 là (11 + √117)/2 hoặc (11 - √117)/2.

A>0 chứ ko phải x>0

a: A=x+3+|x-3|

=x+3+3-x(x<=3)

=6

b:\(B=\sqrt{x^2+4x+4}-\sqrt{x^2}\)

\(=\left|x+2\right|-\left|x\right|\)

=x+2-x=2

c: \(C=\dfrac{\sqrt{x^2-2x+1}}{x-1}\)

\(=\dfrac{\left|x-1\right|}{x-1}=\dfrac{x-1}{x-1}=1\)

\(B=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\) 

a) ĐK: \(x\ne1,x\ge0\)

\(B=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\)

\(B=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right]\cdot\dfrac{\left(x-1\right)^2}{2}\)

\(B=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right]\cdot\dfrac{\left(x-1\right)^2}{2}\)

\(B=\left[\dfrac{x+\sqrt{x}-2\sqrt{x}-2-x+\sqrt{x}-2\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right]\cdot\dfrac{\left(x-1\right)^2}{2}\)

\(B=\dfrac{-2\sqrt{x}}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)^2}{2}\)

\(B=-\sqrt{x}\left(\sqrt{x}-1\right)\) 

\(a,P=\left(\dfrac{2x-1}{x+3}-\dfrac{x}{3-x}-\dfrac{3-10x}{x^2-9}\right):\dfrac{x+2}{x-3}\left(x\ne\pm3;x\ne-2\right)\\ P=\dfrac{2x^2-7x+3+x^2+3x-3+10x}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x+2}\\ P=\dfrac{3x^2+6x}{\left(x-3\right)\left(x+2\right)}=\dfrac{3x\left(x+2\right)}{\left(x-3\right)\left(x+2\right)}=\dfrac{3x}{x-3}\\ b,x^2-7x+12=0\\ \Leftrightarrow\left(x-3\right)\left(x-4\right)=0\\ \Leftrightarrow x=4\left(x\ne3\right)\\ \Leftrightarrow A=\dfrac{3\cdot4}{4-3}=12\\ c,P=\dfrac{3\left(x-3\right)+9}{x-3}=3+\dfrac{9}{x-3}\in Z\\ \Leftrightarrow x-3\inƯ\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\\ \Leftrightarrow x\in\left\{-6;0;2;4;6;12\right\}\)

a) Với x > 0; x ≠ 4,ta có:

Câu 2:

a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)

=>\(2m\ne4\)

=>\(m\ne2\)

b: Thay m=0 vào (d1), ta được:

\(y=\left(0-1\right)x+2=-x+2\)

Thay m=0 vào (d2), ta được:

\(y=\left(3-0\right)x-2=3x-2\)

Vẽ đồ thị:

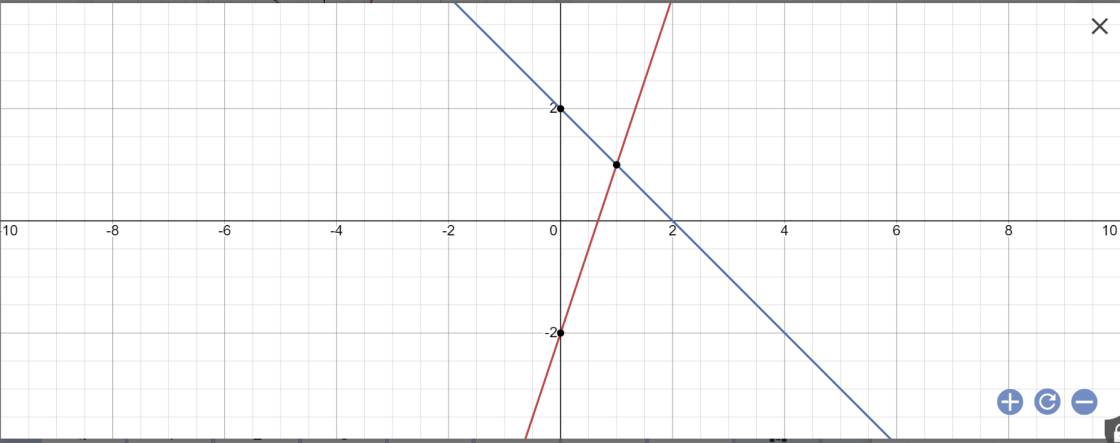
c: Phương trình hoành độ giao điểm là:

3x-2=-x+2

=>3x+x=2+2

=>4x=4

=>x=1

Thay x=1 vào y=3x-2, ta được:

y=3*1-2=3-2=1

d:

Khi m=0 thì (d2): y=3x-2

Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox

y=3x-2 nên a=3

\(tan\alpha=a=3\)

=>\(\alpha\simeq72^0\)

Câu 3:

a: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra OM là đường trung trực của AB

=>OM\(\perp\)AB tại H và H là trung điểm của AB

Xét ΔOAM vuông tại A có AH là đường cao

nên \(OH\cdot OM=OA^2\)

=>\(OH\cdot OM=R^2\)

b: Ta có: AC//OM

OM\(\perp\)AB

Do đó: AB\(\perp\)AC

=>ΔABC vuông tại A

=>ΔABC nội tiếp đường tròn đường kính BC

mà ΔABC nội tiếp (O)

nên O là trung điểm của BC

=>B,O,C thẳng hàng

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>BE\(\perp\)EC tại E

=>BE\(\perp\)CM tại E

Xét ΔMBC vuông tại B có BE là đường cao

nên \(ME\cdot MC=MB^2\)(3)

Xét ΔMBO vuông tại B có BH là đường cao

nên \(MH\cdot MO=MB^2\left(4\right)\)

Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)