tìm các số nguyên dương n, k thỏa mãn:
n/n+50 > kn2/kn3 +100
Những câu hỏi liên quan
Tìm các số nguyên dương n, k thỏa n/n+50 > kn^2/ kn^2 + 100
Tìm các số nguyên dương n lẻ sao cho n-1 là số nguyên dương nhỏ nhất trong các số nguyên dương k thỏa mãn \(\frac{k\left(k+1\right)}{2}\)chia hết cho n
29 tháng 6 2023 lúc 12:15
Tìm tất cả các số nguyên dương k sao cho tồn tại số nguyên dương n thỏa mãn 2n+11 chia hết cho 2k-1.
Để tìm tất cả các số nguyên dương k thỏa mãn điều kiện đã cho, ta sẽ giải phương trình theo n.
2n + 11 chia hết cho 2k - 1 có nghĩa là tồn tại một số nguyên dương m sao cho:
2n + 11 = (2k - 1)m
Chuyển biểu thức trên về dạng phương trình tuyến tính:
2n - (2k - 1)m = -11
Ta nhận thấy rằng nếu ta chọn một số nguyên dương nào đó, ta có thể tìm được một số nguyên dương k tương ứng để phương trình trên có nghiệm. Do đó, ta chỉ cần tìm tất cả các số nguyên dương n thỏa mãn phương trình trên.
Để giải phương trình này, ta có thể sử dụng thuật toán Euclid mở rộng (Extended Euclidean Algorithm). Tuy nhiên, trong trường hợp này, ta có thể tìm được một số giá trị n và k thỏa mãn phương trình bằng cách thử từng giá trị của n và tính giá trị tương ứng của k.
Dưới đây là một số cặp giá trị n và k thỏa mãn phương trình đã cho:
(n, k) = (3, 2), (7, 3), (11, 4), (15, 5), (19, 6), …
Từ đó, ta có thể thấy rằng có vô số giá trị n và k thỏa mãn phương trình đã cho.
Đúng 0
Bình luận (1)
25 tháng 12 2020 lúc 20:06
n3+8n2+13nn3+8n2+13nlà số nguyên tố
Đọc tiếp
là số nguyên tố
1.
\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)
\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)
\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)
\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)
Đặt \(xy=a\Rightarrow0< a\le1\)
\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)
\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)
\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)
\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)
\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)
\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)
Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)
Đúng 1
Bình luận (3)
2.
Đặt \(A=9^n+62\)
Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)
Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)
\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)
Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\) và \(6m+1\)
\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)
\(\Leftrightarrow36m^2=9^n+63\)
\(\Leftrightarrow4m^2=9^{n-1}+7\)
\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)
\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)
Pt ước số cơ bản, bạn tự giải tiếp
Đúng 2
Bình luận (2)
Tìm tất cả các số nguyên dương x,y,z thỏa mãn x!+y!+z!=5.n! ( k! = 1.2.3.4.5.6....k)
Cho các số nguyên dương tùy ý k, n thỏa mãn k
≤
n. Đẳng thức nào dưới đây đúng ?
A
.
C
n
k
C
n
+
1
k
-
1
+
C
n
+
1...
Đọc tiếp
Cho các số nguyên dương tùy ý k, n thỏa mãn k ≤ n. Đẳng thức nào dưới đây đúng ?
A . C n k = C n + 1 k - 1 + C n + 1 k
B . C n k = C n - 1 k - 1 + C n + 1 k
C . C n k = C n - 1 k - 1 + C n k - 1
D . C n k = C n - 1 k - 1 + C n - 1 k
Chọn D
Dựa vào công thức ta có C n k = C n - 1 k - 1 + C n - 1 k
Đúng 0
Bình luận (0)
Với n là số nguyên dương thỏa mãn
A
n
k
+
2
A
n
2
100
(
A
n
k
là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa
x...
Đọc tiếp
Với n là số nguyên dương thỏa mãn A n k + 2 A n 2 = 100 ( A n k là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa x 5 trong khai triển của biểu thức 1 + 3 x 2 n là:
A. 61236
B. 256 x 3
C. 252
D. 61236 x 3
Đáp án D
Phương pháp: Chỉnh hợp chập k của tập hợp có n phần tử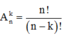 
Cách giải:
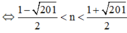
Mà 
Thay lần lượt n = 2;3;4;5;6;7 vào 
n |
2 |
3 |
4 |
5 |
6 |
7 |
k |
Loại |
Loại |
Loại |
Loại |
Loại |
Loại |
Vậy n = 5
Khi đó, 
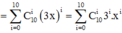
Số hạng chứa
x
5
trong khai triển ứng với i = 5. Số hạng đó là: 
Đúng 0
Bình luận (0)
Với n là số nguyên dương thỏa mãn
A
n
k
+
2
A
n
2
100
(
A
n
k
là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa
x
5
trong khai triển của biểu thức...
Đọc tiếp
Với n là số nguyên dương thỏa mãn A n k + 2 A n 2 = 100 ( A n k là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa x 5 trong khai triển của biểu thức 1 + 3 x 2 n là:
A. 61236
B. 256 x 3
C. 252
D. 61236 x 3
Với k và n là các số nguyên dương tùy ý thỏa mãn k
≤
n, mệnh đề nào dưới đây sai?
A
.
C
n
k
C
n
n
-
k
B
.
C
n
k
A
n...
Đọc tiếp
Với k và n là các số nguyên dương tùy ý thỏa mãn k ≤ n, mệnh đề nào dưới đây sai?
A . C n k = C n n - k
B . C n k = A n k k !
C . C n k - 1 + C n k = C n + 1 k
D . C n k = C n k
Chọn D
Dựa vào lý thuyết hoán vị, chỉnh hợp, tổ hợp
Trắc nghiệm: Dùng máy tính chọn các giá trị cụ thể.
Đúng 0
Bình luận (0)
1. Chứng minh rằng nếu các số nguyên dương x, y thỏa mãn điều kiện x2 + y2 + 2x(y+1) − 2y là số chính phương thì x y.2. Tìm các số nguyên dương n để n4 + 2n3 + 3n3 + 3n + 7 là số chính phương.3. Tìm các số tự nhiên m,n thỏa mãn 2m + 3 n2.4. Tìm các số tự nhiên n để n2 + n + 2 là tích của k số nguyên dương liên tiếp với k ≥ 2.5. Tìm các số tự nhiên n để 36n − 6 là tích của k số nguyên dương liên tiếp với k ≥ 2.6. Tìm số tự nhiên n lớn nhất để 427 +4500 +4n là số chính phương.7. Tìm các số...
Đọc tiếp
1. Chứng minh rằng nếu các số nguyên dương x, y thỏa mãn điều kiện x2 + y2 + 2x(y+1) − 2y là số chính phương thì x = y.
2. Tìm các số nguyên dương n để n4 + 2n3 + 3n3 + 3n + 7 là số chính phương.
3. Tìm các số tự nhiên m,n thỏa mãn 2m + 3 = n2.
4. Tìm các số tự nhiên n để n2 + n + 2 là tích của k số nguyên dương liên tiếp với k ≥ 2.
5. Tìm các số tự nhiên n để 36n − 6 là tích của k số nguyên dương liên tiếp với k ≥ 2.
6. Tìm số tự nhiên n lớn nhất để 427 +4500 +4n là số chính phương.
7. Tìm các số nguyên tố p để 2p - 1 - 1 / p là số chính phương