chứng minh trong 1 tam giác cân, 2 đường trung tuyến thuộc 2 cạnh bên bằng nhau

Những câu hỏi liên quan
Chứng minh hai điều sau:
1/ Trong tam giác cân các đường chủ yếu trùng nhau và ngược lại, tam giác có hai đường chủ yếu bất kì trùng nhau là tam giác cân.
2/ Trong tam giác cân, hai tia phân giác của hai góc kề cạnh đối bằng nhau; hai đường cao thuộc hai cạnh bên bằng nhau; hai trung tuyến thuộc hai cạnh bên bằng nhau.
Ai làm được sẽ nắm vững kiến thức tam giác cân lớp 7.
Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Gọi BM, CN là 2 đường trung tuyến của \(\Delta ABC\)
\( \Rightarrow \)MA = MC = \(\dfrac{1}{2}\)AC; NA = NB = \(\dfrac{1}{2}\)AB
Vì \(\Delta ABC\) cân tại A nên AB = AC ( tính chất)
Do đó, AM = MC = NA = NB
Xét \(\Delta \)ANC và \(\Delta \)AMB, ta có:
AN = AM
\(\widehat A\) chung
AC = AB
\( \Rightarrow \)\(\Delta \)ANC = \(\Delta \)AMB (c.g.c)
\( \Rightarrow \) NC = MB ( 2 cạnh tương ứng)
Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.

Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)
\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).
\(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\) ( tính chất đường trung tuyến trong tam giác)
Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)
Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).
\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).
Xét \(∆BCN\) và \(∆CBM\) có:
+) \(BC\) là cạnh chung
+) \(CN = BM\) (giả thiết)
+) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)
Suy ra \(∆BCN = ∆CBM\) (c.g.c)
\(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).
\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân)
Đúng 0
Bình luận (0)
bài 1: chứng minh 1 tam có 2 đường trung tuyến bằng nhau thì tam giác đó cân
bài 2: chứng minh trong tam giác cân 2 đường cao ứng với 2 cạnh bên và ngược lại có 2 đường cao bằng nhau là tam giác cân
bài 3:chứng minh 2 đường phân giác xuất phát từ 2 đỉnh ở đấy của tam giác cân thì bằng nhau và ngược lại 1 tam giác có 2 đg phân giác bằng nhau thì là tam giác ân
Chứng minh trong một tam giác cân, đường trung tuyến ứng với 2 cạnh bên thì bằng nhau
Chứng minh tam giác bằng nhau theo trường hợp c.h-g.n
Mà chúng là 2 cạnh tương ứng nên bằng nhau
Đúng 0
Bình luận (0)
chứng minh rằng:
a) Trong một tam giác cân,hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau
b) Ngược lại,nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân
#\(N\)
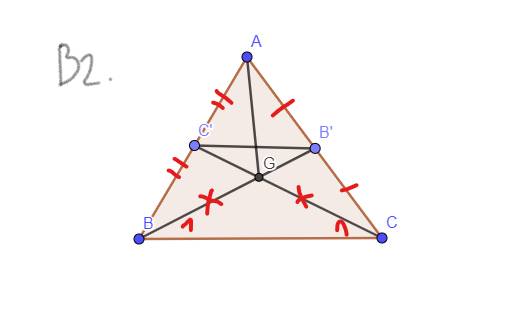
`a,` `GT: AB = AC,` \(\widehat{B}=\widehat{C}\)
`CM: BB' = C``C'`
`BB'` là đường trung tuyến
`-> B'` là trung điểm của `AC`
`-> AB' = B'C`
`C``C'` là đường trung tuyến
`-> C'` là trung điểm của `AB`
`-> AC' = C'B`
Tam giác `ABC` cân tại `A`
`-> AB = AC`
`-> AC' = AB' = C'B = B'C`
Xét Tam giác `BB'C` và Tam giác `C``C'B:`
`C'B = B'C`
\(\widehat{B}=\widehat{C}\)
`BC` chung
`=>` Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`=> BB' = C``C' (2` cạnh tương ứng `) (đpcm)`
`b, GT: AB' = B'C ; AC'=C'B ; C``C' = BB'`
`KL:` Tam giác `ABC` cân
`BB', C``C'` là đường trung tuyến
giả sử: `BB'` cắt `C``C'` tại `G`
`-> G` là trọng tâm của Tam giác `ABC`
`-> GB = 2/3 BB'`
`-> GC = 2/3 C``C'`
`BB' = C``C' -> GB = GC`
`->` Tam giác `GBC` cân tại `G`
`->`\(\widehat{B_1}=\widehat{C_1}\)
Xét Tam giác `BB'C` và Tam giác `C``C'B` có:
`BB' = C``C'`
\(\widehat{B_1}=\widehat{C_1}\)
`BC` chung
`=>`Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`-> BC' = B'C`
`-> 1/2 AB = 1/2 AC`
`-> AB = AC`
`->` Tam giác `ABC` cân tại `A (đpcm)`.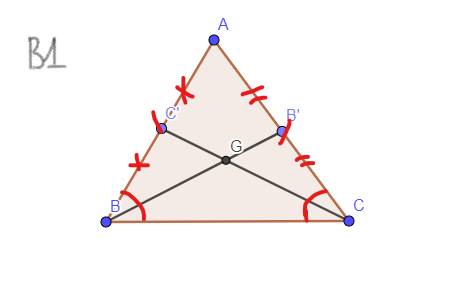
Đúng 2
Bình luận (0)
a: ΔABC cân tại A có BM,CN là các trung tuyến
Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
b: Gọi G là giao của BM và CN
=>G là trọng tâm của ΔABC
=>GB=2/3BM; GC=2/3CN
mà BM=CN
nên GB=GC
=>góc GBC=góc GCB
Xét ΔNBC và ΔMCB có
NC=MB
BC chung
góc NCB=góc MBC
=>ΔNBC=ΔMCB
=>góc ABC=góc ACB
=>ΔBAC cân tại A
Đúng 2
Bình luận (1)
Chứng minh định lí: trong một tam giác cân , hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.?
Và
Hãy chứng minh định lí đảo của định lí trên: nếu hai tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân
Chứng minh rằng 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân thì bằng nhau
chứng minh trong 1 tam giác cân 2 đg trung tuyến ứng với hai cạnh bên thì bằng nhau
1. Hãy chứng minh định lý: trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
2. Hãy chứng minh định lí: nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Giúp mình với!
Ai nhanh 3 tick
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)
Đúng 0
Bình luận (0)
Chứng minh Trong tam giác cân , hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau
hình tự vẽ
tam giác cân ABC tại A
=>AB=AC, góc B=góc C
các đường trung tuyến BE và CF (E thuộc AC, F thuộc AB)
Xét tam giác BEC và tam giác CFB
BC chung
góc C= góc B
EC=FB (EC=1/2AC=1/2AB=FB)
=>tam giác BEC=CFB (c.g.c)
=>BE=CF
Vậy trong tam giác cân hai đường trung tuyến ứng với hai cạn bên thì bằng nhau (BE=CF)
Đúng 0
Bình luận (0)
Tk mk đi mk học lớp 8 và nằm trong đội tuyển toan lun đó tk đi rồi mk giải cho
Đúng 0
Bình luận (0)
GoiBF ; CE là các đường trung tuyến của∆ABC
Ta có AF=FC; AF+FC=AC
AE=EB; AE+EB=AB
AB=AC
Suy ra AE=AF
Xét ∆ABF và ∆ACE có
AE=AF
AB=AC
Chung góc A
=) ∆ABF=∆ACE ( c-g-c )
=) BF=CE. ( đpcm )
Đúng 0
Bình luận (0)






















