Cho \(\Delta ABC\)cân tại A .Lấy điểm M nằm trong \(\Delta ABC\)sao cho MB<MC. Chứng minh rằng \(\widehat{AMB}\)> \(\widehat{AMC}\)
Giúp mình với ~!!! Mình cần gấp
Cho \(\Delta ABC\)vuông cân tại A. Điểm M nằm trong tam giác sao cho MA=2cm, MB=3cm và \(\widehat{AMC}\)=135. Tính MC
trên nửa mặt phẳng bờ AM không chứa điểm B vẽ tam giác ADM vuông cân tại A
Ta có : \(\widehat{DMC}=\widehat{AMC}-\widehat{AMD}=90^o\)
\(\Rightarrow\)\(\Delta ADC=\Delta AMC\left(c.g.c\right)\)
\(\Rightarrow\)DC = MB = 3cm
Xét \(\Delta AMD\)vuông tại A, theo định lí Py-ta-go, ta có :
MD2 = MA2 + AD2 = 22 + 22 = 8
Xét \(\Delta MCD\)vuông tại M , theo định lí Py-ta-go, ta có :
CD2 = MD2 + MC2 \(\Rightarrow\)MC2 = CD2 - MD2 \(\Rightarrow\)MC2 = 32 - 8 = 1 \(\Rightarrow\)MC = 1 cm
Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh \(\widehat {ABC}\)=\(\widehat {ACB}\).
Xét \(\Delta AMB\) và \(\Delta AMC\)có:
AB = ? (?)
MB = MC (?)
AM là cạnh ?
Vậy \(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
Suy ra \(\widehat {ABC}\)=\(\widehat {ACB}\)

Xét \(\Delta AMB\) và \(\Delta AMC\).có:
AB = AC ( do tam giác ABC cân tại A )
MB = MC ( do M là trung điểm BC )
AM là cạnh chung
=>\(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
=>\(\widehat {ABC}\)=\(\widehat {ACB}\)( 2 góc tương ứng)
Cho \(\Delta\)ABC cân tại A . Điểm M nằm bên trong tam giác sao cho MA=2cm; MB=3cm và \(\widehat{AMC}\)= 135\(^0\). Tính MC
Answer:
Trên nửa mặt phẳng bờ AM không chứa B xác định điểm D sao cho tam giác ADM vuông cân tại A
Lúc này AD = AM = 2cm và góc AMD = 45 độ
=> Góc DMC = góc AMC - góc AMD = 135 độ - 45 độ = 90 độ
Ta xét tam giác ADC và tam giác AMB:
AC = AB (gt)
AD = AM
Góc DAC = góc MAB
=> Tam giác ADC = tam giác AMB (c.g.c)
=> BM = CD = 3cm
Ta xét tam giác ADM vuông tại A, áp dụng định lý Pytago:
\(MD^2=MA^2+AD^2=2^2+2^2=8\)
Ta xét tam giác MDC vuông tại M, áp dụng định lý Pytago:
\(CD^2=MD^2+MC^2\Rightarrow3^2=8+MC^2\Rightarrow MC=1cm\)
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
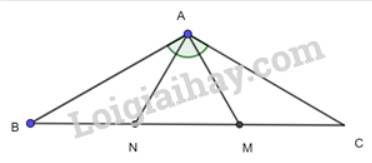
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.
\(\left(1\right)\Delta ABC\) vuông cân tại A. M là 1 điểm nằm trong tam giác ABC. Sao cho MA= 2cm , MB = 3cm , góc AMC = 135o . Tính MC
(2) Tam giác ABC vuông cân tại A . M là 1 điểm nằm trong tam giác ABC. Sao cho MC : MA : MB = 1:2:3 . Tính góc AMC
Mong được mấy anh chị CTV hoặc quản lí giúp đỡ ạ!
Cho \(\Delta ABC\) vuông cân tại A, M là điểM nằM trong \(\Delta ABC\) sao cho \(\text{M}A:\text{M}B:\text{M}C=2:3:1\).
Tính \(\widehat{AMC}\)
Mk cần gấp lắM ạ ##@@##
Cho \(\Delta ABC\) cân tại A, điểm M nằm trong tam giác sao cho MB<MC. Chứng minh rằng góc AMB > góc AMC
Cho \(\Delta ABC\) cân tại B, có \(\widehat{ABC}\)=800 . Lấy điểm I nằm trong tam giác sao cho \(\widehat{IAC}\) =100 và \(\widehat{ICA}\)=300 . Tính số đo \(\widehat{AIB}\)?
Cho \(\Delta ABC\) cân tại B , có \(\widehat{ABC}=80^o\) . Lấy điểm I nằm trong tam giác sao cho \(\widehat{IAC}=10^o\) và \(\widehat{ICA}=30^o\) . Tính số đo \(\widehat{AIB}\) .
Do ΔABC cân tại B => A = C = \(\dfrac{180^o-80^o}{2}=50^o\)
=> góc BAI = 50o - 10o = 40o
góc BCI = 50o - 30o = 20o
=> \(IBC=\dfrac{1}{3}ABI\Rightarrow IBC=\dfrac{80^o}{3+1}=20^o;ABI=80^o-20^o=60^o\)
\(\Leftrightarrow AIB=180^o-40^o-60^o=80^o\)