1.Cho tam giác ABC có hai đường trung tuyến BM và CN Gọi K là giao điểm của BM và CN Chứng minh tam giác ABC cân

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Vẽ BM và CN là 2 đường trung tuyến. a/ Chứng minh: BM = CN b/Chứng minh: Tứ giác BNMC là hình thang cân. c/ Gọi I là giao điểm của BM và CN. Chứng minh: AI vuông góc với MN
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Tham khảo:
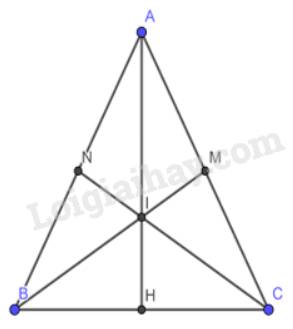
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A.BM lÀ phÂn giác góc ABC,CN là phân giác góc ACB
a) chứng minh BM=CN
b) gọi I là giao điểm của BM và CN,K là giao điểm của AI và MN. Chứng minh tam giác IBC cân và K là trung điểm của MN
giải nhanh giùm mình đc k ạ mai mình phải nộp r mà vẫn chx hiểu
a: Xét ΔABM và ΔACN co
góc ABM=góc ACN
AB=AC
góc BAM chung
=>ΔABM=ΔACN
=>BM=CN
b: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I
=>IB=IC
mà AB=AC
nên AI là trung trực của BC
=>AI vuông góc BC
=>AI vuông góc MN tại K
=>K là trung điểm của MN
Đúng 1
Bình luận (0)
cho tam giác abc có ab< ac. bm và cn là hai đường trung tuyến của tam giác abc. chứng minh rằng cn> bm
1)Cho tam giác ABC, có 2 đường trung tuyến BM và CN cắt nhau tại G. Chứng minh: BM+ CN > 3232BC
2)Cho tam giác ABC, D là trung điểm AC. Trên BD lấy E sao cho BE=2ED. F thuộc tia đối của tia DE sao cho BF=2BE. K là trung điểm CF,G là giao điểm EK và AC. Chứng minh
a) G là trọng tâm tam giác EFC
b) Tính GEGKGEGK,GCDC
1:
Xét ΔBAC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>BG=2/3BM và CG=2/3CN
BG+CG>BC
=>2/3BM+2/3CN>BC
=>2/3(BM+CN)>BC
=>BM+CN>3/2BC
2:
BF=2BE
=>EF=BE
=>EF=2ED
=>D là trung điểm của EF
Xét ΔFEC có
CD,EK là trung tuyến
CD cắt EK tại G
=>G là trọng tâm
b: G là trọng tâm của ΔFEC
=>GE/GK=1/2 và GC/DC=2
Đúng 1
Bình luận (0)
1. Cho tam giác ABC, gọi BM và CN lần lượt là các đường trung tuyến sao cho BM vuông góc với CN. Chứng minh cotA 2 (cotB + cotC)2. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông cân tại A có H là trung điểm của BC, D là hình chiếu vuông góc của H trên AC và M là trung điểm HD. Đường thẳng BD đi qua E(0;4) và AC đi qua điểm F(-1;5). Tìm tọa độ các đỉnh A, B, C biết đường thẳng AM có phương trình x - 3y + 14 0 và A có hoành độ âm
Đọc tiếp
1. Cho tam giác ABC, gọi BM và CN lần lượt là các đường trung tuyến sao cho BM vuông góc với CN. Chứng minh cotA = 2 (cotB + cotC)
2. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông cân tại A có H là trung điểm của BC, D là hình chiếu vuông góc của H trên AC và M là trung điểm HD. Đường thẳng BD đi qua E(0;4) và AC đi qua điểm F(-1;5). Tìm tọa độ các đỉnh A, B, C biết đường thẳng AM có phương trình x - 3y + 14 = 0 và A có hoành độ âm
Cho tam giác ABC cân tại A. Gọi M, N thứ tự là trung điểm của AC và AB. gọi G là giao điểm của BM và CN. Chứng minh: a) tam giác AMN cân, b) BM = CN, c) tam giác GBC cân
a, Do \(NA=NB=\frac{1}{2}AB\)
\(AM=MC=\frac{1}{2}AC\)
Mà \(AB=AC\)\(\Rightarrow NA=MA;NB=MC\)\(\Rightarrow\)\(\Delta AMN\)cân tại \(A\)
b, Xét \(\Delta ANC\)và \(\Delta AMB\)có:
\(\widehat{BAC}chung\)
\(AB=AC\)
\(AN=AM\)(câu a)
\(\Rightarrow\Delta ANC=\Delta AMB\)
\(\Rightarrow BM=CN\)
c, Xét \(\Delta NBC\) và\(\Delta MCB\) có:
\(BCchung\)
NB = MC ( câu a)
NC = MB ( câu b)
=>\(\Delta NBC=\Delta MCB\)=>\(\widehat{GBC}=\widehat{GCB}\)=>\(\Delta GBC\) cân tại C
TYM cho chị nhé <3
Đúng 1
Bình luận (0)
Cho tam giác ABC, các đường trung tuyến BM và CN. Trên cạnh BC lấy điểm D và E sao cho BD=DE=EC. Gọi H là giao điểm của AD và BM, gọi K là giao điểm của AE và CN. Chứng minh rằng ba đường thẳng MK,NH và BC đồng quy.
1)Cho tam giác ABC, có 2 đường trung tuyến BM và CN cắt nhau tại G. Chứng minh: BM+ CN dfrac{3}{2}BC2)Cho tam giác ABC, D là trung điểm AC. Trên BD lấy E sao cho BE2ED. F thuộc tia đối của tia DE sao cho BF2BE. K là trung điểm CF,G là giao điểm EK và AC. Chứng minha) G là trọng tâm tam giác EFCb) Tính dfrac{GE}{GK},dfrac{GC}{DC}
Đọc tiếp
1)Cho tam giác ABC, có 2 đường trung tuyến BM và CN cắt nhau tại G. Chứng minh: BM+ CN > \(\dfrac{3}{2}\)BC
2)Cho tam giác ABC, D là trung điểm AC. Trên BD lấy E sao cho BE=2ED. F thuộc tia đối của tia DE sao cho BF=2BE. K là trung điểm CF,G là giao điểm EK và AC. Chứng minh
a) G là trọng tâm tam giác EFC
b) Tính \(\dfrac{GE}{GK}\),\(\dfrac{GC}{DC}\)
giúp mik với đang cần gấp lém :((
ét-o-ét
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A vẽ hai đường trung tuyến BM và CN cắt nhau tại G
1 chứng minh BM=CN
2 chứng minh AG là tia phân giác của góc BAC
3 chứng minh MN song song với BC
4 gọi H là giao điểm của AG và BC chứng minh AH vuông góc với BC
















