Giúp mình câu 6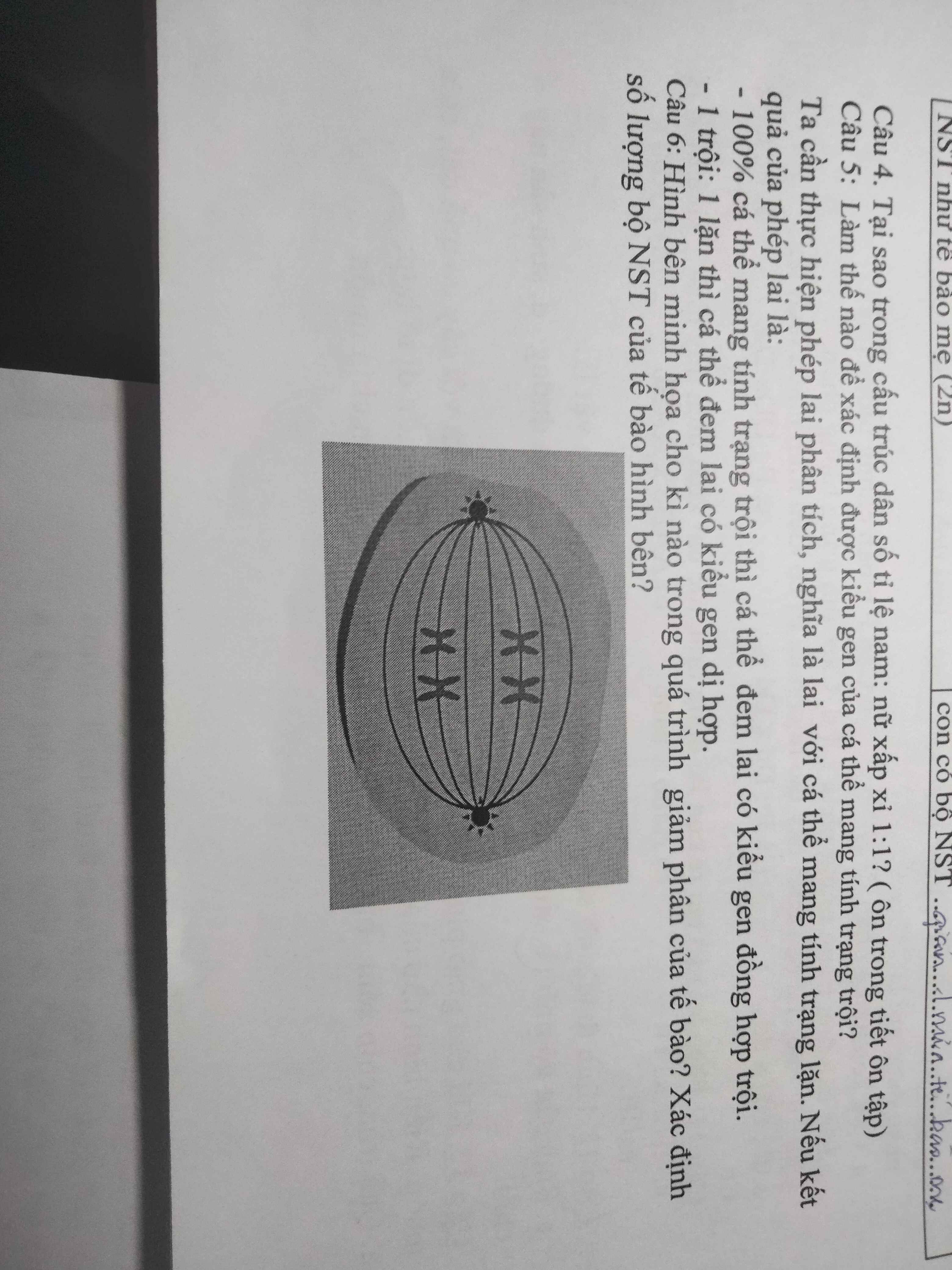

Những câu hỏi liên quan
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
Giúp mình câu 5 6 làm theo kiểu mảng giúp mình
GIÚP MÌNH CÂU 6 --> CÂU 10
GIÚP MÌNH CÂU 6 --> CÂU 8
6 going out for a walk
7 to get married next month
8 remembering people's names
Đúng 1
Bình luận (0)
giúp mình câu 4 câu 6
Đọc tiếp
giúp mình câu 4 câu 6
Làm giúp mình câu 2, 4, 6. Nếu các bạn k làm hết cũng đc thì lm 1 câu giúp mình.
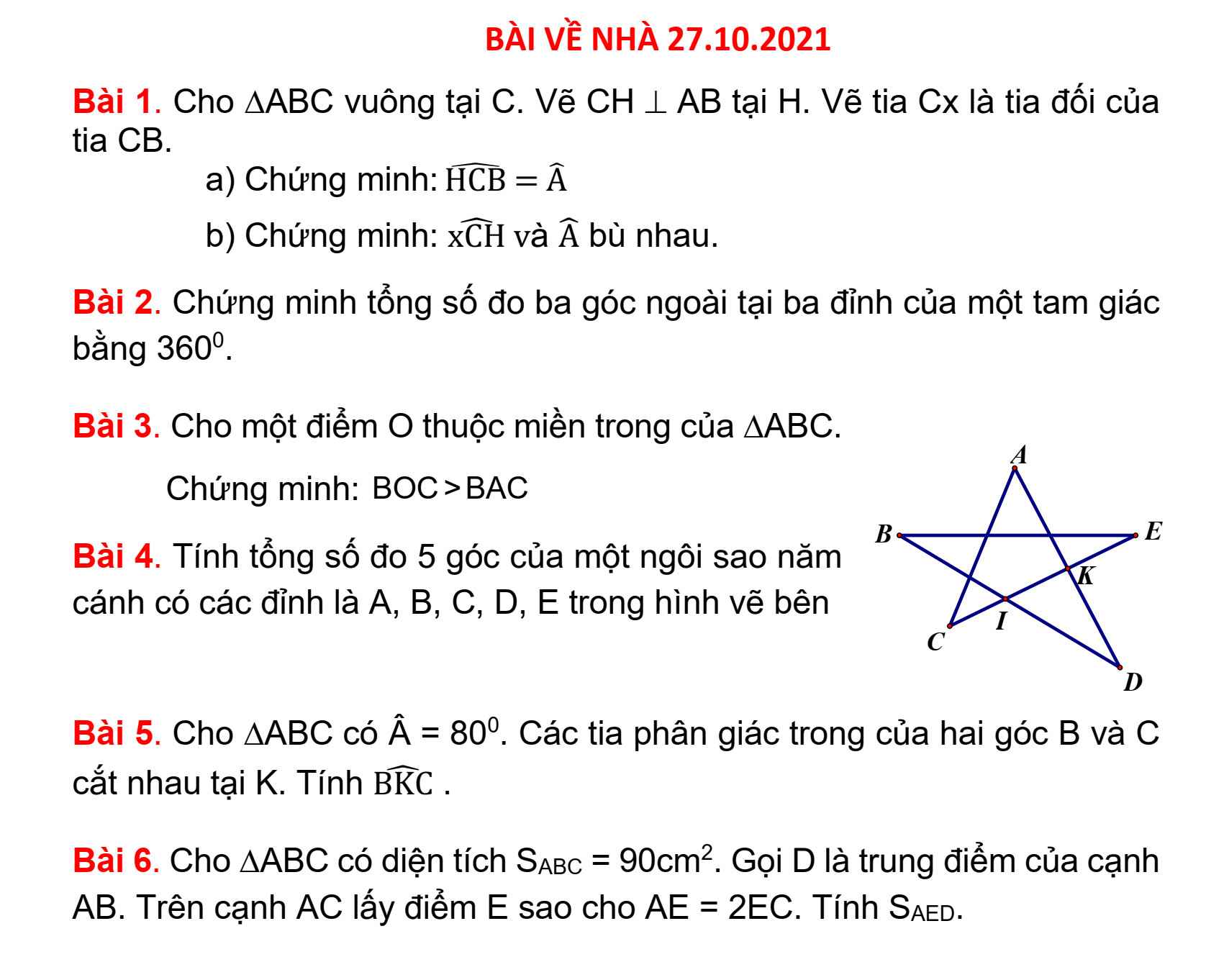
Bài 5:
\(\widehat{BKC}=180^0-\left(\widehat{KBC}+\widehat{KCB}\right)\)
\(=180^0-\dfrac{180^0-80^0}{2}\)
\(=180^0-50^0=130^0\)
Đúng 0
Bình luận (0)
13: \(cos^2x-\sqrt3\cdot\sin2x=1+\sin^2x\)
=>\(cos^2x-\sin^2x-\sqrt3\cdot\sin2x=1\)
=>\(cos2x-\sqrt3\cdot\sin2x=1\)
=>\(\frac12\cdot cos2x-\frac{\sqrt3}{2}\cdot\sin2x=\frac12\)
=>\(\sin\left(\frac{\pi}{6}-2x\right)=\frac12\)
=>\(\sin\left(2x-\frac{\pi}{6}\right)=-\frac12\)
=>\(\left[\begin{array}{l}2x-\frac{\pi}{6}=-\frac{\pi}{6}+k2\pi\\ 2x-\frac{\pi}{6}=\pi+\frac{\pi}{6}+k2\pi=\frac76\pi+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=k2\pi\\ 2x=\frac43\pi+k2\pi\end{array}\right.\)
=>\(\left[\begin{array}{l}x=k\pi\\ x=\frac23\pi+k\pi\end{array}\right.\)
12: \(\sin2x-2\cdot\sin^2x=0\)
=>\(2\cdot\sin x\cdot cosx-2\cdot\sin^2x=0\)
=>\(2\cdot\sin x\left(cosx-\sin x\right)=0\)
=>\(\sin x\cdot\left(\cos x-\sin x\right)=0\)
TH1: sin x=0
=>\(x=k\pi\)
TH2: cos x-sin x=0
=>\(\sin x=cosx\)
=>\(\sin x=\sin\left(\frac{\pi}{2}-x\right)\)
=>\(\left[\begin{array}{l}x=\frac{\pi}{2}-x+k2\pi\\ x=\pi-\frac{\pi}{2}+x+k2\pi=\frac{\pi}{2}+x+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=\frac{\pi}{2}+k2\pi\\ \frac{\pi}{2}+k2\pi=0\left(vôlý\right)\end{array}\right.\)
=>\(x=\frac{\pi}{4}+k\pi\)
11: \(\sin2x+2\cdot\sin^2x=0\)
=>\(2\cdot\sin x\cdot cosx+2\cdot\sin^2x=0\)
=>\(2\cdot\sin x\cdot\left(cosx+\sin x\right)=0\)
=>\(\sin x\cdot\left(cosx+\sin x\right)=0\)
TH1: \(\sin x=0\)
=>\(x=k\pi\)
TH2: sin x+cos x=0
=>\(\sqrt2\cdot\sin\left(x+\frac{\pi}{4}\right)=0\)
=>\(\sin\left(x+\frac{\pi}{4}\right)=0\)
=>\(x+\frac{\pi}{4}=k\pi\)
=>\(x=k\pi-\frac{\pi}{4}\)
5: \(2\cdot cos^2x-2\cdot cos2x-4\cdot\sin x\cdot cosx+1=0\)
=>\(2\cdot cos^2x-1-2\cdot cos2x-2\cdot\sin2x+2=0\)
=>\(cos2x-2\cdot cos2x-2\cdot\sin2x+2=0\)
=>\(-cos2x-2\cdot\sin2x=-2\)
=>\(2\cdot\sin2x+cos2x=2\)
=>\(\sin2x\cdot\frac{2}{\sqrt5}+cos2x\cdot\frac{1}{\sqrt5}=\frac{2}{\sqrt5}\)
=>\(\sin\left(2x+\alpha\right)=cos\left(\alpha\right)=\sin\left(\frac{\pi}{2}-\alpha\right)\)
=>\(\left[\begin{array}{l}2x+\alpha=\frac{\pi}{2}-\alpha+k2\pi\\ 2x+\alpha=\pi-\frac{\pi}{2}+\alpha+k2\pi=a+\frac{\pi}{2}+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=-2\alpha+\frac{\pi}{2}+k2\pi\\ 2x=\frac{\pi}{2}+k2\pi\end{array}\right.\)
=>\(\left[\begin{array}{l}x=-\alpha+\frac{\pi}{4}+k\pi\\ x=\frac{\pi}{4}+k\pi\end{array}\right.\)
4: \(2\cdot cos^2x-3\sqrt3\cdot\sin2x-4\cdot\sin^2x+4=0\)
=>\(2\cdot\frac{1+cos2x}{2}-3\sqrt3\cdot\sin2x-4\cdot\frac{1-cos2x}{2}+4=0\)
=>\(1+cos2x-3\sqrt3\cdot\sin2x-2\left(1-cos2x\right)+4=0\)
=>\(1+cos2x-3\sqrt3\cdot\sin2x-2+2\cdot cos2x+4=0\)
=>\(-3\sqrt3\cdot\sin2x+3\cdot cos2x+3=0\)
=>\(-\sqrt3\cdot\sin2x+cos2x=-1\)
=>\(\sqrt3\cdot\sin2x-cos2x=1\)
=>\(\sin2x\cdot\frac{\sqrt3}{2}-cos2x\cdot\frac12=\frac12\)
=>\(\sin\left(2x-\frac{\pi}{6}\right)=\frac12\)
=>\(\left[\begin{array}{l}2x-\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\ 2x-\frac{\pi}{6}=\pi-\frac{\pi}{6}+k2\pi=\frac56\pi+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=\frac{\pi}{3}+k2\pi\\ 2x=\pi+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{\pi}{6}+k\pi\\ x=\frac{\pi}{2}+k\pi\end{array}\right.\)
3: \(4\sqrt3\cdot\sin x\cdot cosx+4\cdot cos^2x-2\cdot\sin^2x=\frac52\)
=>\(2\sqrt3\cdot\sin2x+4\cdot\frac{1+cos2x}{2}-2\cdot\frac{1-cos2x}{2}=\frac52\)
=>\(2\sqrt3\cdot\sin2x+2+2\cdot cos2x-1+cos2x=\frac52\)
=>\(2\sqrt3\cdot\sin2x+3\cdot cos2x=\frac52-1=\frac32\)
=>\(\sin2x\cdot2+cos2x\cdot\sqrt3=\frac{\sqrt3}{2}\)
=>\(\sin2x\cdot\frac{2}{\sqrt7}+cos2x\cdot\frac{\sqrt3}{\sqrt7}=\frac{\sqrt3}{2\sqrt7}\)
=>\(\sin\left(2x+\alpha\right)=\frac{\sqrt3}{2\sqrt7}=\frac{\sqrt{21}}{14}\)
=>\(\left[\begin{array}{l}2x+\alpha=\arcsin\left(\frac{\sqrt{21}}{14}\right)+k\pi\\ 2x+\alpha=\pi-\arcsin\left(\frac{\sqrt{21}}{14}\right)+k\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=\arcsin\left(\frac{\sqrt{21}}{14}\right)+k\pi-\alpha\\ 2x=\pi-\arcsin\left(\frac{\sqrt{21}}{14}\right)-\alpha+k\pi\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac12\cdot\arcsin\left(\frac{\sqrt{21}}{14}\right)+\frac{k\pi}{2}-\frac{\alpha}{2}\\ x=\frac{\pi}{2}-\frac12\cdot\arcsin\left(\frac{\sqrt{21}}{14}\right)-\frac{\alpha}{2}+\frac{k\pi}{2}\end{array}\right.\)
Đúng 0
Bình luận (0)
Mng giúp mình câu 5. Cho mình hỏi câu 6 mình đúng ko. Cảm ơn bạn 🤩
 CÂU 4 CÂU 5 CÂU 6
CÂU 4 CÂU 5 CÂU 6
GIÚP MÌNH VỚI Ạ
Đổi: \(40\%=\dfrac{2}{5}\)
Số học sinh giỏi Anh bằng : \(1-\dfrac{3}{7}-\dfrac{2}{5}=\dfrac{6}{35}\) ( số học sinh trong câu lạc bộ )
Số học sinh trong câu lạc bộ là: \(48:\dfrac{6}{35}=280\) ( học sinh )
Số học sinh giỏi Toán là: \(280.\dfrac{3}{7}=120\) ( học sinh )
Số em giỏi Văn là: \(280-120-48=112\) ( học sinh )
Đúng 2
Bình luận (0)
Bài 4:
Số học sinh của câu lạc bộ là:
\(48:\left(1-\dfrac{3}{7}-\dfrac{2}{5}\right)=48:\dfrac{6}{35}=48\cdot\dfrac{35}{6}=280\)(bạn)
Số học sinh giỏi Toán là:
\(280\cdot\dfrac{3}{7}=120\)(bạn)
Số học sinh giỏi Văn là:
\(280\cdot\dfrac{2}{5}=112\)(bạn)
Đúng 1
Bình luận (0)
Câu 6:
Ta có
\(\dfrac{1}{1^2}=1;\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};\dfrac{1}{4^2}< \dfrac{1}{3.4};...;\dfrac{1}{50^2}< \dfrac{1}{49.50}\)
⇒ A \(=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{50^2}< \) \(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\)
⇒ A < \(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
⇒ A < \(1+\dfrac{99}{100}\)
⇒ A < \(1+\dfrac{99}{100}< 1+\dfrac{100}{100}\)
⇒ A < 2
Đúng 1
Bình luận (0)
Giúp mình câu 4c câu 5 câu 6 với thanks 
Bài 5:
a,Phương trình tọa độ của vật
\(x=30t+\dfrac{1}{2}\cdot2\cdot t^2=30t+t^2\left(m,s\right)\)
Tọa độ của vật tại thười điểm t=6s
\(x=30\cdot6+\dfrac{1}{2}\cdot2\cdot6^2=216\left(m,s\right)\)
b,Vật sẽ dừng lại sau
\(t=\dfrac{v-v_0}{a}=\dfrac{0-30}{-2}=15\left(s\right)\)
Quãng đường đi được trong thời gian trên
\(s=30\cdot15+15^2=675\left(m\right)\)
c, Phương trình vận tốc của vật
\(v=v_0+at=30-2t\)
Vận tốc của vật tại thời điểm trước khi dừng 2 s
\(v=30-2.\left(15-2\right)=4\left(\dfrac{m}{s}\right)\)
Đúng 3
Bình luận (0)
Bài 4
Đổi 36 km/h=10 m/s
a, Gia tốc của đoàn tàu
\(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{0-10^2}{2\cdot200}=-0,25\left(\dfrac{m}{s^2}\right)\)
b,Quãng đường đi được của vật sau 10s hãm phanh
\(s=v_0t+\dfrac{1}{2}at^2=10\cdot10+\dfrac{1}{2}\cdot0,25\cdot10^2=112,5\left(m\right)\)
Vận tốc lúc đó là
\(v=v_0+at=10-0,25\cdot10=7,5\left(\dfrac{m}{s}\right)\)
c, Tàu dừng lại sau
\(t=\dfrac{v-v_0}{a}=\dfrac{0-10}{-0.25}=40\left(s\right)\)
Đúng 1
Bình luận (0)



























