Tìm tất cả các giá trị của m để (m-1)x²-2(m-2)x+m-3=0 có 2 nghiệm x1, x2 thỏa: x1+x2+x1.x2<1

Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để pt x^2-(m-1)*x+4*m^2-m=0 có hai nghiệm trái dấu X1, X2 thỏa mãn điều kiện
2*(X1+X2)+3*x1*x2<2
Cho phương trình: x2-(m-1)x-m-2=0. Tìm tất cả các giá trị của m để pt có 2 nghiệm phân biệt x1, x2 thỏa mãn x2+x1-x2=4-m
giải chi tiết cho phương trình: x2 - 2(m-1)x+2m-3=0 tìm tất cả các giá trị của m để phương trình có 2 nghiệm x1,x2 thỏa mãn x1 +m=2x2+1
x² - 2(m - 2)x + m² - 5m - 4 = 0 (1) m là tham số a giải phương trình 1 với M = 1 b tìm tất cả các giá trị của tham số m để phương trình 1 có 2 nghiệm phân biệt x1 x2 thỏa mãn x1 bình + X2 bình bằng -3 x1 x2 - 4
a: Khi m=1 thì (1): x^2-2(1-2)x+1^2-5-4=0
=>x^2+2x-8=0
=>(x+4)(x-2)=0
=>x=2 hoặc x=-4
b: Δ=(2m-4)^2-4(m^2-5m-4)
=4m^2-16m+16-4m^2+20m+16
=4m+32
Để pt có hai nghiệm phân biệt thì 4m+32>0
=>m>-8
x1^2+x2^2=-3x1x2-4
=>(x1+x2)^2+x1x2+4=0
=>(2m-4)^2+m^2-5m-4+4=0
=>4m^2-16m+16+m^2-5m=0
=>5m^2-21m+16=0
=>(m-1)(5m-16)=0
=>m=16/5 hoặc m=1
Đúng 0
Bình luận (0)
Cho phương trình: x 2 - 2(m - 3)x + 5 - m = 0
a) Giải phương trình khi m = 1.
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x1 < x2 < 1.
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0 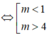
Do x1 < x2 < 1
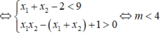
Đúng 0
Bình luận (0)
Với tất cả giá trị nào của tham số m thì phương trình
(
m
-
10
)
x
2
-
2
(
m
-
2
)
x
+
m
-
3
0
có hai nghiệm
x
1
,
x
2
thỏa mãn
x
1
+
x...
Đọc tiếp
Với tất cả giá trị nào của tham số m thì phương trình ( m - 10 ) x 2 - 2 ( m - 2 ) x + m - 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 + x 1 . x 2 < 1
A. 1<m<3.
B. 1<m<2.
C. m>2.
D. m>3.
Cho phương trình x2 - (m +1)x +2m -8 =0 (1), m là tham số.
a) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn x12 + x22 + ( x1 - 2)(x2 -2) =11
Δ=(m+1)^2-4(2m-8)
=m^2+2m+1-8m+32
=m^2-6m+33
=(m-3)^2+24>=24
=>Phương trình luôn có hai nghiệm pb
x1^2+x2^2+(x1-2)(x2-2)=11
=>(x1+x2)^2-2x1x2+x1x2-2(x1+x2)+4=11
=>(m+1)^2-(2m-8)-2(m+1)+4=11
=>m^2+2m+1-2m+8-2m-2-7=0
=>m^2-2m-8=0
=>(m-4)(m+2)=0
=>m=4 hoặc m=-2
Đúng 2
Bình luận (0)
cho phương trình x^2 - x + 1 +m = 0 tìm các giá trị của m để phương trình trên có hai nghiệm x1, x2 thỏa mãn x1*x2*(x1*x2 - 2) = 3*(x1 + x2)
Theo hệ thức Vi-ét ta có:
x1+x2=\(-\frac{-1}{1}=1\)
x1x2=\(\frac{1+m}{1}=1+m\)
=> x1x2(x1x2-2)=3(x1+x2)
<=> (1+m)(1+m-2)=3
<=> m2-1=3
<=>m2=4
<=> m=-2 hoặc m =2 (loại)
Vậy m = -2
Đúng 0
Bình luận (0)
Cho phương trình \(x^2-2\left(m+1\right)x+m^2+2m=0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1,x2(x1<x2)
thoa man: \(\left|x1\right|=3\left|x2\right|\)
\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho pt x2-2x-m=0. Tìm tất cả giá trị của m để pt có 2 nghiệm x1,x2 thỏa mãn x1<x2<2.
Để phương trình có 2 nghiệm phân biệt :
\(\Delta>0< =>\left(-2\right)^2-4\left(-m\right)>0\)
\(< =>4+4m>0\)
\(< =>4m>-4\)
\(< =>m>-1\)


















