BÀI 1:
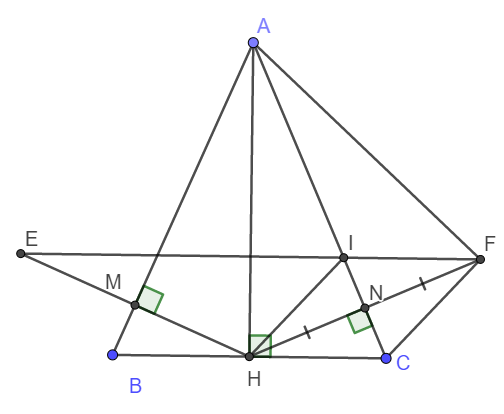
Cho ∆ ABC cân tại A. Kẻ AH ⊥ BC (H ∈ BC), kẻ HM ⊥ AB(M ∈ AB), HN⊥ AC( N ∈ AC). a) Chứng minh : HM= HN b) Trên tia đối của NH lấy điểm F sao cho NF=NH. C/m: FC⊥ FA c) Qua H kẻ đường thẳng song song với FC cắt AC tại I. C/m: IF∕∕ BC d) Trên tia đối của tia MH lấy điểm E sao cho ME=MH.C/m: 3 điểm E,I,F thẳng hàng.