+ Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2

⇒ –b/2a = –3/2 ⇒ b = 3a (1)

+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)

⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).

Thay b = 3a ở (1) vào biểu thức (2) ta được:

9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.

Vậy parabol cần tìm là y = –1/3x2 – x + 2.

(P) đi qua điểm A (−2; 4) nên 4 = a. ( − 2 ) 2 = 4a  a = 1

Vậy phương trình parabol (P) là y   =   x 2 .

Để (P) tiếp xúc với (d) thì phương trình hoành độ giao điểm

x 2 = 2 (m – 1)x – (m – 1)có nghiệm kép

↔ ∆ ’ = [ − ( m – 1 ) ] 2   − m + 1 = 0 ↔ m 2 – 2m + 1 − m + 1 = 0 ↔ m 2 – 3m + 2 = 0 ↔ m=1 hoặc m=2

Nếu m = 1 thì hoành độ giao điểm là x = 0. Vậy tiếp điểm là (0; 0)

Nếu m = 2 thì hoành độ giao điểm là x = 1. Vậy tiếp điểm là (1; 1)

Đáp án: C

+ Parabol y = ax2 + bx + 2 đi qua M(1 ; 5)

⇒ 5 = a.12 + b.1 + 2 ⇒ a + b = 3 (1) .

+ Parabol y = ax2 + bx + 2 đi qua N(–2; 8)

⇒ 8 = a.( –2)2 + b.( –2) + 2 ⇒ 4a – 2b = 6 (2).

Từ (1) và (2) suy ra: a = 2; b = 1.

Vậy parabol cần tìm là y = 2x2 + x + 2.

a: Thay x=-4 và y=-4 vào (P), ta được:

16a=-4

=>a=-1/4

=>y=-1/4x^2

b: PTHĐGĐ là:

-1/4x^2=1/4x-3

=>x^2=-x+12

=>x^2+x-12=0

=>(x+4)(x-3)=0

=>x=3 hoặc x=-4

=>y=-1/4*(-4)^2=4 hoặc y=-1/4*3^2=-9/4

Đáp án A

+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)

⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)

+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4

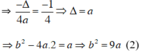
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.

Phương trình có hai nghiệm b = 12 hoặc b = –3.

Với b = 12 thì a = 16.

Với b = –3 thì a = 1.

Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.

Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:

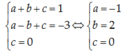
Vậy (P): y = -x² + 2x

Chọn C.

Trục đối xứng là x=-4

=>\(\dfrac{-\left(-6\right)}{2a}=-4\)

=>\(\dfrac{-6}{2a}=4\)

=>\(2a=-\dfrac{3}{2}\)

=>\(a=-\dfrac{3}{4}\)

=>(P): \(y=-\dfrac{3}{4}x^2-6x+c\)

Phương trình hoành độ giao điểm là:

\(-\dfrac{3}{4}x^2-6x+c=0\)

\(\text{Δ}=\left(-6\right)^2-4\cdot\dfrac{-3}{4}\cdot c\)

\(=36+3c\)

Để (P) cắt trục Ox tại 2 điểm phân biệt thì Δ>0

=>3c+36>0

=>3c>-36

=>c>-12

Theo Vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{6}{-\dfrac{3}{4}}=6\cdot\dfrac{-4}{3}=-8\\x_1\cdot x_2=\dfrac{c}{a}=c:\dfrac{-3}{4}=-\dfrac{4}{3}c\end{matrix}\right.\)

Để (P) cắt trục Ox tại 2 điểm có độ dài bằng 4 thì \(\left|x_1-x_2\right|=4\)

=>\(\sqrt{\left(x_1-x_2\right)^2}=4\)

=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=4\)

=>\(\sqrt{\left(-8\right)^2-4\cdot\dfrac{-4c}{3}}=4\)

=>\(\sqrt{64+\dfrac{16c}{3}}=4\)

=>\(\dfrac{16}{3}\cdot c+64=16\)

=>\(\dfrac{16}{3}\cdot c=-48\)

=>\(c=-48:\dfrac{16}{3}=-48\cdot\dfrac{3}{16}=-9\left(nhận\right)\)