Cho tam giác đều ABC có độ dài cạnh bằng a. Gọi M là một điểm nằm ở mièn trung của tam giác. MI, MP, MQ theo thứ tự lần lượt là khoảng cách từ M đến cách cạnh BC, AB, AC. CM MI + MP + MQ không đổi

Những câu hỏi liên quan
Cho tam giác đều ABC có độ dài cạnh bằng a. Gọi M là một điểm nằm ở mièn trung của tam giác. MI, MP, MQ theo thứ tự lần lượt là khoảng cách từ M đến cách cạnh BC, AB, AC. gọi O là trung điểm canh BC . các điểm D ,E theo thứ tự chuyển động trên các cạnh AB,AC sao cho góc DOE60 .a CM MI + MP + MQ không đổib chứng minh DE luôn tiếp xúc với 1 dường tròn cố định
Đọc tiếp
Cho tam giác đều ABC có độ dài cạnh bằng a. Gọi M là một điểm nằm ở mièn trung của tam giác. MI, MP, MQ theo thứ tự lần lượt là khoảng cách từ M đến cách cạnh BC, AB, AC. gọi O là trung điểm canh BC . các điểm D ,E theo thứ tự chuyển động trên các cạnh AB,AC sao cho góc DOE=60 .
a CM MI + MP + MQ không đổi
b chứng minh DE luôn tiếp xúc với 1 dường tròn cố định
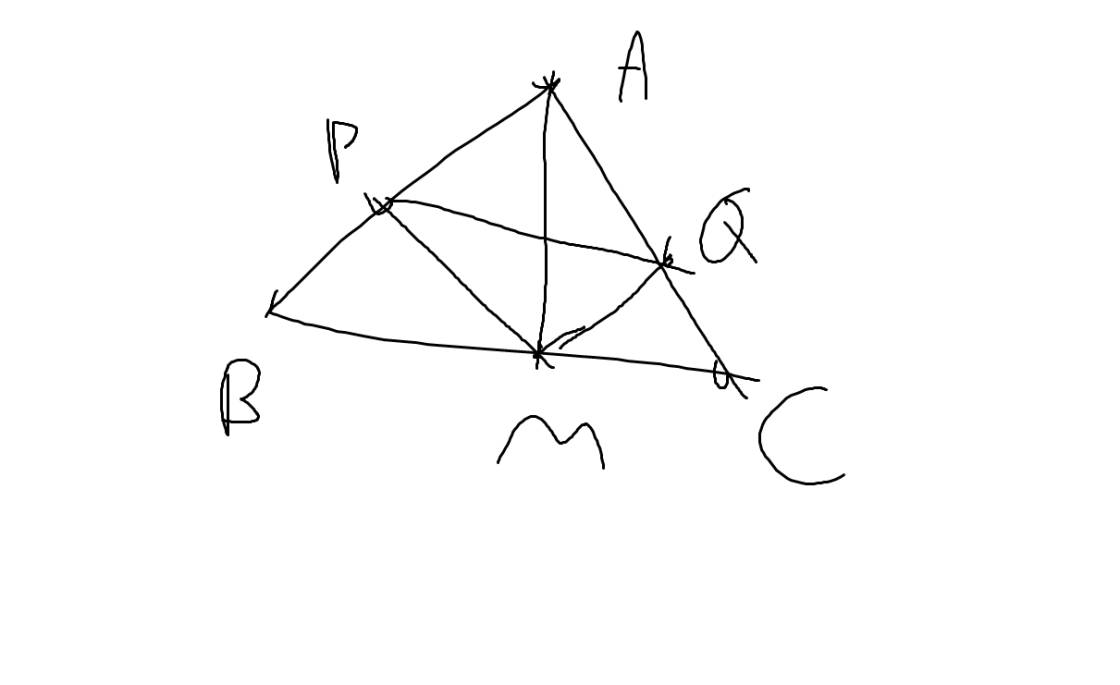
Cho tam giác đều ABC có độ dài cạnh bằng a. Gọi M là 1 điểm nằm trong tam giác. MI,MP,MQ theo thứ tự là khoảng cách từ M đến các cạnh BC,AB,AC. Gọi O là trung điểm của cạnh BC. Các điểm D và E theo thứ tự chuyển động trên các cạnh AB và AC sao cho widehat{DOE}60^o.
a) Chứng minh: MI+MP+MQ không đổi.
b) Chứng minh: Đường thẳng DE luôn tiếp xúc với một đường tròn cố định.
c) Xác định vị trí của D và E để diện tích tam giác DOE đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo a.
Đọc tiếp
Cho tam giác đều \(ABC\) có độ dài cạnh bằng \(a\). Gọi \(M\) là 1 điểm nằm trong tam giác. \(MI,MP,MQ\) theo thứ tự là khoảng cách từ \(M\) đến các cạnh \(BC,AB,AC\). Gọi \(O\) là trung điểm của cạnh \(BC\). Các điểm \(D\) và \(E\) theo thứ tự chuyển động trên các cạnh \(AB\) và \(AC\) sao cho \(\widehat{DOE}=60^o\).
\(a\)) Chứng minh: \(MI+MP+MQ\) không đổi.
\(b\)) Chứng minh: Đường thẳng \(DE\) luôn tiếp xúc với một đường tròn cố định.
\(c\)) Xác định vị trí của \(D\) và \(E\) để diện tích tam giác \(DOE\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo \(a\).
Cho tam giác đều ABC. Đường cao AH.M là một điểm thuộc cạnh BC(M khác A và B).từ M kẻ MP,MQ lần lượt vuông góc với AB,AC.
a/Chứng minh MP+MQ không đổi
b/Gọi O là trung điểm của AM.tứ giác POQH là hình gì
c/tìm vị trí của M trên BC để độ dài PQ là ngắn nhất
Cho tam giác ABC đều M bất kì trong tam giác ABC.Từ M kẻ các đường vuông góc đến các cạnh AB,BC,AC lần lượt cắt các cạnh đấy tại N,P,Q a C m MN MP MQ không đổi khi m thay đổib 3 cạnh MN ,MP,MQ là 3 cạnh của tam giác
Cho tam giác ABC đều M bất kì trong tam giác ABC.Từ M kẻ các đường vuông góc đến các cạnh AB,BC,AC lần lượt cắt các cạnh đấy tại N,P,Q a)C/m MN+MP+MQ không đổi khi m thay đổi
b) 3 cạnh MN ,MP,MQ là 3 cạnh của tam giác
Cho tam giác ABC cân tại A, đường cao BH và điểm M bất kì trên BC. Gọi P và Q theo thứ tự là hình chiếu của M trên AB và AC. Trên tia đối của MQ lấy R sao cho MRMPa, cm BHQR là hình chữ nhật b, có nhận xét j về độ lớn của tổng MP+MQ khi M di độngc, cm AP+AQAB+AHd, xét góc xAy hãy tìm các điểm thuộc tập hợp M nằm trong góc đó sao cho khoảng cách từ M đến 2 cạnh của 2 góc M cho trước
Đọc tiếp
Cho tam giác ABC cân tại A, đường cao BH và điểm M bất kì trên BC. Gọi P và Q theo thứ tự là hình chiếu của M trên AB và AC. Trên tia đối của MQ lấy R sao cho MR=MP
a, cm BHQR là hình chữ nhật
b, có nhận xét j về độ lớn của tổng MP+MQ khi M di động
c, cm AP+AQ=AB+AH
d, xét góc xAy hãy tìm các điểm thuộc tập hợp M nằm trong góc đó sao cho khoảng cách từ M đến 2 cạnh của 2 góc M cho trước
Cho tam giác cân ABC. Từ điểm M trên cạnh đáy BC vẽ các đường MP, MQ lần lượt vuông góc với AB, AC. CM: MP+MQ không phụ thuộc vào vị trí của M trên cạnh BC
Ta co \(MP=MB.\sin\widehat{B},MQ=MC.\sin\widehat{C}\)
=> \(MP+MQ=\left(MB+MC\right).\sin\widehat{B}=BC.\sin\widehat{B}=const\)
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC.
Xem chi tiết
a, Chứng minh rằng MP = MQ và AP = AQ.
b, Đường thẳng PQ có vuông góc với AM không? Vì sao?
VẼ HÌNH GIÚP MÌNH NHA. CẢM ƠN Ạ
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ
Đúng 2
Bình luận (0)
Cho tam giác ABC đều có cạnh bằng a. Gọi O là trung điểm của BC. Một góc xOy bằng 60o quay quanh điểm O sao cho hai cạnh Ox, Oy luôn cắt AB và AC lần lượt tại M và N.a) cm: Tam giác OBM đồng dạng với tam giác NCO.b) cm: BC24BM.CN.c) Khoảng cách từ điểm O đến MN không đổi khi Ox; Oy thay đổi.d) Từ O vẽ đường thẳng d bất kì cắt AB; AC tại P; Q.CMR: dfrac{1}{AP}+dfrac{1}{AQ} không đổi.
Đọc tiếp
Cho tam giác ABC đều có cạnh bằng a. Gọi O là trung điểm của BC. Một góc xOy bằng 60o quay quanh điểm O sao cho hai cạnh Ox, Oy luôn cắt AB và AC lần lượt tại M và N.
a) cm: Tam giác OBM đồng dạng với tam giác NCO.
b) cm: BC2=4BM.CN.
c) Khoảng cách từ điểm O đến MN không đổi khi Ox; Oy thay đổi.
d) Từ O vẽ đường thẳng d bất kì cắt AB; AC tại P; Q.
CMR: \(\dfrac{1}{AP}+\dfrac{1}{AQ}\) không đổi.
a.
a.
\(\widehat{BMO}+\widehat{B}+\widehat{BOM}=\widehat{BOM}+\widehat{MON}+\widehat{CON}=180^0\)
\(\Rightarrow\widehat{BMO}=\widehat{CON}\) (do \(\widehat{B}=\widehat{MON}=60^0\))
\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\widehat{C}=60^0\\\widehat{BMO}=\widehat{CON}\end{matrix}\right.\) \(\Rightarrow\Delta OBM\sim\Delta NCO\) (g.g)
b.
Từ câu a \(\Rightarrow\dfrac{OB}{CN}=\dfrac{BM}{OC}\Rightarrow OB.OC=BM.CN\Rightarrow\dfrac{BC}{2}.\dfrac{BC}{2}=BM.CN\Rightarrow...\)
Đúng 1
Bình luận (0)
c.
Lần lượt kẻ OD và OE vuông góc MN và AB.
Do O cố định \(\Rightarrow\) OE cố định
Từ câu a ta có: \(\dfrac{BM}{OC}=\dfrac{OM}{ON}\Rightarrow\dfrac{BM}{OM}=\dfrac{OC}{ON}=\dfrac{OB}{ON}\) (1)
Đồng thời \(\widehat{B}=\widehat{MON}=60^0\) (2)
(1);(2) \(\Rightarrow\Delta OBM\sim\Delta NOM\left(c.g.c\right)\Rightarrow\widehat{BMO}=\widehat{OMN}\)
\(\Rightarrow\Delta_VOME=\Delta_VOMD\left(ch-gn\right)\)
\(\Rightarrow OD=OE\), mà OE cố định \(\Rightarrow OD\) cố định
Đúng 1
Bình luận (0)
d.
Không mất tính tổng quát, giả sử d cắt AB, AC như hình vẽ bên dưới
Trên tia AC lấy G sao cho \(AG=AP\Rightarrow\Delta APG\) đều (tam giác cân 1 góc 60 độ)
\(\Rightarrow\) AO đồng thời là trung trực PG
\(\Rightarrow OP=OG\Rightarrow\Delta OBP=\Delta OCG\left(c.c.c\right)\)
\(\Rightarrow\widehat{QOC}=\widehat{BOP}\left(đối-đỉnh\right)=\widehat{COG}\Rightarrow OC\) là phân giác \(\widehat{QOG}\) và OA là phân giác ngoài đỉnh O tam giác OQG
\(\Rightarrow\dfrac{CQ}{CG}=\dfrac{OQ}{OG}=\dfrac{AQ}{AG}\) theo định lý phân giác \(\Rightarrow\dfrac{CQ}{AQ}=\dfrac{CG}{AG}\)
\(\Rightarrow\dfrac{AC-AQ}{AQ}=\dfrac{AG-AC}{AG}\Rightarrow\dfrac{AC}{AQ}-1=1-\dfrac{AC}{AG}\)
\(\Rightarrow AC\left(\dfrac{1}{AQ}+\dfrac{1}{AG}\right)=2\Rightarrow\dfrac{1}{AQ}+\dfrac{1}{AG}=\dfrac{2}{AC}\)
\(\Rightarrow\dfrac{1}{AQ}+\dfrac{1}{AP}=\dfrac{2}{AC}\) không đổi
Đúng 1
Bình luận (0)
Xem thêm câu trả lời















