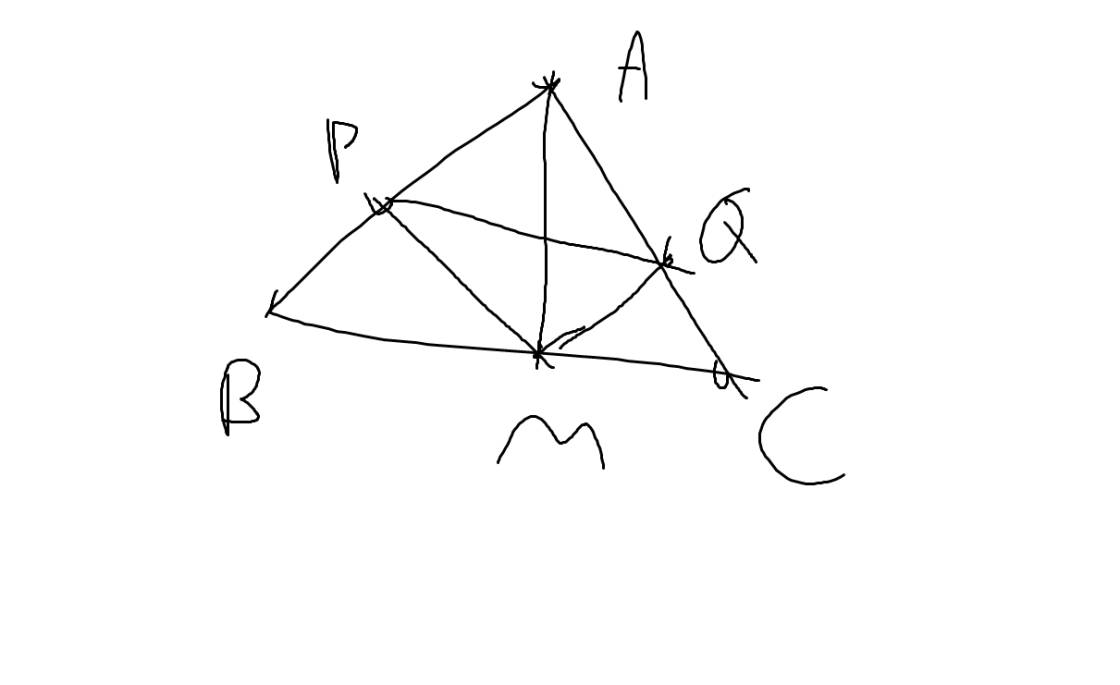
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ
Cho tam giác ABC nhọn, AB > AC, đường cao BE và CF cắt nhau tại H. Gọi M là trung điểm BC. Trên tia đối của các tia AM và AC lần lượt lấy P và Q sao cho AP=AM VÀ AQ=AC.
C/m: AH vuông góc với PQ
Cho tam giác cân ABC (AB = AC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N. Chứng minh rằng:
a) DM = EN
b) Đường thẳng BC cắt MN tại trung điểm I của MN.c) Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên BC
Cho tam giác ABC có ba góc nhọn, gọi M là trung điểm của AC. Đường vuông góc với AB kẻ từ A cắt đường thẳng BM tại D. Trên tia BM lấy điểm E sao cho M là trung điểm của DE. CHứng minh rằng CE vuông góc với AB
Các bạn giúp mình vs ạ
cho tam giác ABC cân tại A. Trên cạnh BC lần lượt là BC lần lượt lấy các điểm M và N ( M nằm giữa B và N ) sao cho BM = CN. Kẻ MH vuông góc với AB; NK vuông góc với AC. Chứng minh:
a) Tam giác MHB = tam giác NKC
b) AH = AK
c) tam giác AMN cân tại A
Cho tam giác ABC cân tại A. Trên 2 cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = AN. Kẻ AH vuông góc với BC, H ∈ BC
a. Chứng minh tam giác ABH = tam giác ACH
b. Chứng minh BN=CM
c. Nếu cho cạnh AH=8cm, AB= 10cm. Tính cạnh BC
ho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm K sao cho BK=BA. Gọi M là trung điểm của đoạn thẳng AK. a) Chứng minh: ∆AMB=∆KMB b) Đường thẳng BM cắt đường thẳng AC tại D. Chứng minh: DK vuông góc với BC. c) Trên tia đối của tia AB lấy điểm H sao cho ah=kc chứng minhh d k thẳng hàng
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Trên tia đối của tia AB lấy điểm E sao cho AC = AE a) chứng minh tam giác ABC = tam giác ADE b) gọi M , N lần lượt là trung điểm của BC và DE , chứng minh AM = AN c) tính số đo của góc MAN
