Gấp một mảnh giấy hình chữ nhật ABCD như hình vẽ sao cho điểm D trùng với điểm E (E thuộc BC) Tính CE, biết AD=10cm,AB=8 cm
Có một mảnh bìa hình chữ nhật ABCD với AB=4a, AD=2a. Người ta đánh dấu M là trung điểm của AB, N và P là các điểm thuộc CD sao cho DN = CP = a. Sau đó người ta cuốn mảnh bìa lại sao cho cạnh BC trùng với cạnh AD tạo thành một hình trụ. Tính thể tích của tứ diện AMNP với các đỉnh A, M, N, P nằm trên hình trụ vừa tạo thành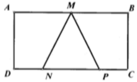
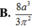
Có một miếng bìa hình chữ nhật ABCD với AB=3 và AD=6. Trên cạnh AD lấy điểm E sao cho AE=2, trên cạnh BC lấy điểm F là trung điểm BC
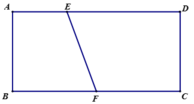
Cuốn miếng bìa lại sao cho cạnh AB và DC trùng nhau để tạo thành mặt xung quanh của một hình trụ. Khi đó tính thể tích V của tứ diện ABEF.
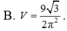
cho hình bình hành ABCD có độ dài các cạnh AB=6 cm BC=4cm trên cạnh AB lấy một điểm E sao cho AE=2 cm Đường rharng CE cắt cạnh AD kéo dài tại F a Chứng minh AFE ~ BCE b Tính độ dài EF biết CE=5cm c Điểm E nằm trên AB phải thỏa mãn điều kiện gì thì S AFE= S BCE/4
a: Xét ΔEAF và ΔEBC có
góc EAF=góc EBC
góc AEF=góc BEC
=>ΔEAF đồng dạng với EBC
b: ΔEAF đồng dạng với ΔEBC
=>EF/EC=AF/BC=AE/EB
=>EF/5=2/4=1/2
=>EF+2,5cm
cho hình chữ nhật ABCD có AB=8cm, AD=6cm. Gọi M là giao điểm của AC và BD. Trên cạnh DC lấy điểm E sao cho ME vuông góc với BD. Tính độ dài ME
ΔADC vuông tại D
=>\(AC^2=AD^2+DC^2\)
=>\(AC^2=8^2+6^2=100\)
=>AC=10(cm)
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>M là trung điểm chung của AC và BD và AC=BD
=>MD=MB=MA=MC=AC/2=5(cm)
Xét ΔDME vuông tại M và ΔDCB vuông tại C có
\(\widehat{MDE}\) chung
Do đó: ΔDME đồng dạng với ΔDCB
=>\(\dfrac{ME}{CB}=\dfrac{DM}{DC}\)
=>\(\dfrac{ME}{6}=\dfrac{5}{8}\)
=>\(ME=3,75\left(cm\right)\)
Cho tam giác ABC có góc A=90, AB=3cm, BC=10cm. D là một điểm thuộc cạnh BC, I là trung điểm của cạnh AC, E là điểm đối xứng với D qua I.
a) Điểm D ở vị trí nào trên BC thì AECD là hình chữ nhật? Giải thích? Vẽ hình minh họa.
b) Điểm D ở vị trí nào trên BC thì AECD là hình thoi? Giải thích? Vẽ hình minh họa và tính độ dài cạnh của hình thoi.
Cho hình chữ nhật ABCD, biết AB = 8cm, AD = 12cm. Trên cạnh BC lấy điểm E sao cho: BC = 3 × BE, lấy điểm F là trung điểm của cạnh CD. Tính diện tích tứ giác AECF theo đơn vị xăng-ti-mét vuông.
Cho hình chữ nhật ABCD có chu vi là 60 cm, chiều dài AB gấp rưỡi chiều rộng BC. Lấy một điểm M trên cạnh BC sao cho MB = 2 MC. Nối AM kéo dài cắt DC kéo dài tại điểm E. Nối B với E ; D với M
a) Tính diện tích hình chữ nhật ABCD.
b) So sánh diện tích tam giác MBE và diện tích tram giác MCD
c) Gọi O là giao điểm của AM và BD. Tính tỉ số \(\dfrac{OB}{OD}\)
a) Cho tam giác \(ABC\) có \(AB = 12cm,AC = 15cm,BC = 18cm\). Trên cạnh \(AB\), lấy điểm \(E\) sao cho \(AE = 10cm\). Trên cạnh \(AC\), lấy điểm \(F\) sao cho \(AF = 8cm\) (hình 18a). Tính độ dài đoan thẳng \(EF\).
b) Trong Hình 18b, cho biết \(FD = FC,BC = 9dm,DE = 12dm,AC = 15dm,MD = 20dm.\)
Chứng minh rằng \(\Delta ABC\backsim\Delta MED\).
a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).
Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b)
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
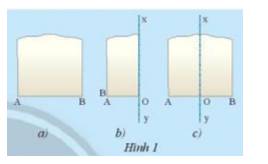
Sau khi gấp A trùng với B thì điểm gấp trên cạnh AB là O
\( \Rightarrow \) AO = BO \( \Rightarrow \)O là trung điểm AB
Vì 2 mép của tờ giấy song song với nhau nên khi gấp đôi đường gấp ở giữa (xy) cũng song song với 2 cạnh của tờ giấy .
Mà 2 cạnh của tờ giấy vuông góc với AB nên xy cũng vuông góc với AB
