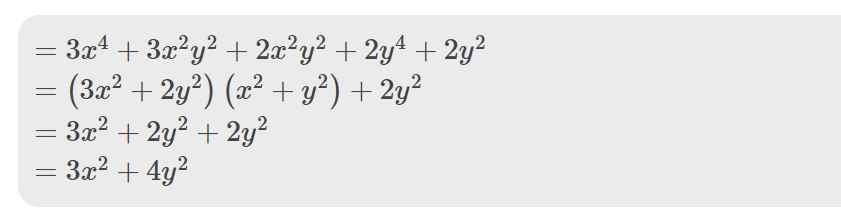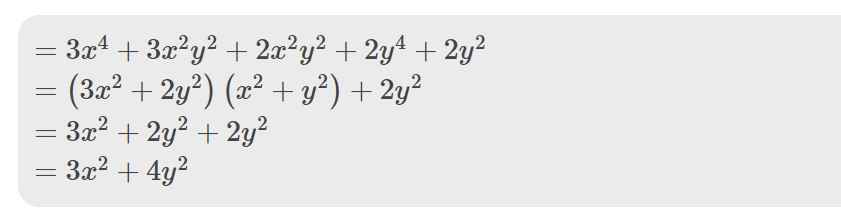tinh gia tri bieu thuc 5x^2y-4xy^2tai x=-2;y=-1

Những câu hỏi liên quan
Cho:x ^2-2xy+2y^2-2x+6y+5=0.Tinh gia tri bieu thuc:3x^2y-1/4xy
Từ \(x^2-2xy+2y^2-2x+6y+5=0\)
\(\Rightarrow\left(x^2-2xy-2x+y^2+2y+1\right)+\left(y^2+4y+4\right)=0\)
\(\Rightarrow\left(x-y-1\right)^2+\left(y+2\right)^2=0\)
\(\Rightarrow\left\{\begin{matrix}\left(x-y-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)\(\Rightarrow\left\{\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Thay vào ta có: \(\frac{3x^2y-1}{4xy}=\frac{3\cdot\left(-1\right)^2\cdot\left(-2\right)-1}{4\cdot\left(-1\right)\cdot\left(-2\right)}=-\frac{7}{8}\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho:x ^2-2xy+2y^2-2x+6y+5=0.Tinh gia tri bieu thuc:3x^2y-1/4xy
ta có : \(x^2-2xy+2y^2-2x+6y+5=0\)
<=>\(\left(x^2+y^2+1-2xy+2y-2x\right)+\left(y^2+4y+4\right)=0\)
<=>\(\left(x-y-1\right)^2+\left(y+2\right)^2=0\)
<=> x-y-1=0 và y+2=0
=> y=-2;x=-1
Vậy \(3x^2y-\frac{1}{4}xy=-6,5\)
Đúng 0
Bình luận (0)
tinh gia tri cac bieu thuc sau:3x^4+5x^2y^2+2y^4+2y^2biet rang x^2+y^2=1
\(=3x^4+3x^2y^2+2x^2y^2+2y^4+2y^2\)
\(=\left(3x^2+2y^2\right)\left(x^2+y^2\right)+2y^2\)
\(=3x^2+2y^2+2y^2\)
\(=3x^2+4y^2\)
Đúng 0
Bình luận (0)
tinh gia tri bieu thuc:
a,3x^4+5x^2y^2+2y^4+2y^2 biet rang x^2+y^2=1
tinh gia tri bieu thuc:
a,3x^4+5x^2y^2+2y^4+2y^2 biet rang x^2+y^2=1
tinh gia tri bieu thuc:
a,3x^4+5x^2y^2+2y^4+2y^2 biet rang x^2+y^2=1
tinh gia tri bieu thuc:
a,3x^4+5x^2y^2+2y^4+2y^2 biet rang x^2+y^2=1
x^2=a;y^2=b( Đk:a,b không âm)
Từ giả thiết suy ra a+b=2
=>3x^4+5x^2y^2+2y^4+2y^2
=3a^2+5ab+2b^2+2b
=(3a^2+3ab)+(2ab+2b^2)+2b
=3a(a+b)+2b(a+b)+2b
=(a+b)(3a+2b)+2b
=2(3a+2b)+2b
=2(2a+2b)+2a+2b
=4.2+2.2=12
Đúng 0
Bình luận (0)
tinh gia tri bieu thuc:
a,3x^4+5x^2y^2+2y^4+2y^2 biet rang x^2+y^2=1
tinh gia tri cua bieu thuc:
3x^4+5x^2y^2+2y^4+2y^2 biet rang x^2+y^2=1
x^2=a;y^2=b(Đk:a,b không âm)
Từ giả thiết suy ra a+b=2
=>3x^4+5x^2y^2+2y^4+2y^2
=3a^2+5ab+2b^2+2b
=(3a^2+3ab)+(2ab+2b^2)+2b
=3a(a+b)+2b(a+b)+2b
=(a+b)(3a+2b)+2b
=2(3a+2b)+2b
=2(2a+2b)+2a+2b
=4.2+2*\.2=12
Đúng 0
Bình luận (0)