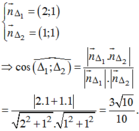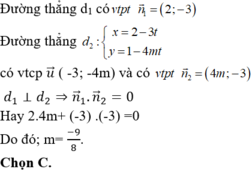Tìm cosin của góc giữa 2 đường thẳng △1: 2x+3y-10=0 và △2: 2x-3y+4=0

Những câu hỏi liên quan
1. Tìm cosin góc giữa 2 đg thẳng denta 1 : 10x +5y -10 và denta 2 : x 2+t ; y 1-t
2. Tìm cosin góc giữa 2 đg thẳng denta 1: x +2y -√20 và denta 2: x - y 0
3. Cặp đg thẳng là phân giác của các góc hợp bởi 2 đg thẳng denta 1 : 3x +4y +10 và denta 2: x -2y +40
4. Tìm cosin góc giữa 2 đg thẳng denta 1 : 2x +3y -100 và denta 2: 2x -3y +40
5. Cho đg thẳng d : x 2+t ; y 1-3t và 2 điểm A(1;2) , B(-2;m). Định m để A và B nằm cùng phía đối với d.
Đọc tiếp
1. Tìm cosin góc giữa 2 đg thẳng denta 1 : 10x +5y -1=0 và denta 2 : x = 2+t ; y = 1-t
2. Tìm cosin góc giữa 2 đg thẳng denta 1: x +2y -√2=0 và denta 2: x - y =0
3. Cặp đg thẳng là phân giác của các góc hợp bởi 2 đg thẳng denta 1 : 3x +4y +1=0 và denta 2: x -2y +4=0
4. Tìm cosin góc giữa 2 đg thẳng denta 1 : 2x +3y -10=0 và denta 2: 2x -3y +4=0
5. Cho đg thẳng d : x =2+t ; y = 1-3t và 2 điểm A(1;2) , B(-2;m). Định m để A và B nằm cùng phía đối với d.
1. Tìm cosin góc giữa 2 đg thẳng denta 1 : 10x +5y -1=0 và denta 2 : x = 2+t ; y = 1-t
\(\Delta\left(1\right):10x+5y-1=0\)
\(\Delta\left(2\right):\left\{{}\begin{matrix}x=2+t\\y=1-t\end{matrix}\right.\)
\(\Delta\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}t=x-2\\y=1-\left(x-2\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t=x-2\\y=1-x+2\end{matrix}\right.\Leftrightarrow x+y-3=0\)
Ta có phương trình tổng quát của \(\Delta\left(2\right)\)là \(x+y-3=0\)
\(cos\left(\Delta\left(1\right),\Delta\left(2\right)\right)=\frac{\left|a_1.a_2+b_1.b_2\right|}{\sqrt{a_1^2+b_1^2}\sqrt{a_2^2+b_2^2}}\)
\(=\frac{\left|10+5\right|}{\sqrt{1+1}.\sqrt{100+25}}=\frac{15}{5\sqrt{10}}\)
Bấm SHIFT COS\(\left(\frac{15}{5\sqrt{10}}\right)\)=o'''
\(=18^o26'5,82''\)
bài 2,3,4 tương tự vậy.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng có phương trình lần lượt là
2
x
−
2
y
−
z
0
và
x
+
3
y
+
z
−
1
0
. Tính cosin của góc giữa đường thẳng d và trục Oy. A.
3
35
B.
3
23...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng có phương trình lần lượt là 2 x − 2 y − z = 0 và x + 3 y + z − 1 = 0 . Tính cosin của góc giữa đường thẳng d và trục Oy.
A. 3 35
B. 3 23
C. 3 74
D. 3 6
Tính góc giữa 2 đường thẳng 2x+4y-1=0 và x-3y+1=0
2x+4y-1=0
=>VTPT là (2;4)
x-3y+1=0
=>VTPT là (1;-3)
\(cos\left(d1;d2\right)=\dfrac{\left|2\cdot1+\left(-4\right)\cdot3\right|}{\sqrt{2^2+4^2}\cdot\sqrt{1^2+\left(-3\right)^2}}=\dfrac{\sqrt{2}}{2}\)
=>\(\widehat{\left(d1;d2\right)}=45^0\)
Đúng 1
Bình luận (0)
chọn và giải ra luôn nhé Trong mặt phẳng Oxy, phương trình đường thẳng d đi qua A(1;-2) và vuông góc với đường thẳng ∆:3x-2y+x=0 là A. 3x-2y-7=0 B.2x+3y+4=0 C.x+3y+5=0 D.2x+3y-3=0
Tìm cosin góc giữa 2 đướng thẳng
∆
1
:
2
x
+
y
+
1
0
và
∆
2
:
x
2
+
t
y
1
-...
Đọc tiếp
Tìm cosin góc giữa 2 đướng thẳng ∆ 1 : 2 x + y + 1 = 0 và ∆ 2 : x = 2 + t y = 1 - t
A. 10 10
B. 3/10
C. 3/5
D. 3 10 10
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10 0 và
d
2
:
x
2
-
3
t
y
1
-
4
m
t...
Đọc tiếp
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
![]()
![]()
![]()
![]()
Đường thẳng d đi qua điểm M(1, 2) và song song với đường thẳng delta: 2x+3y-12=0 có phương trình tổng quát là:
a. 4x+6y+1=0 b.2x+3y-8=0
c. 4x-3y-8=0 c. 2x+3y+8=0
Xem thêm câu trả lời
Tìm góc giữa 2 đường thẳng △1: 2x-y-10=0 và △2: x-3y+9=0
\(\overrightarrow{n_{d1}}=\left(2;-1\right)\) ; \(\overrightarrow{n_{d2}}=\left(1;-3\right)\)
\(cos\left(d_1;d_2\right)=\frac{\left|2.1+\left(-1\right).\left(-3\right)\right|}{\sqrt{2^2+\left(-1\right)^2}.\sqrt{1^2+\left(-3\right)^2}}=\frac{5}{5\sqrt{2}}=\frac{\sqrt{2}}{2}\)
\(\Rightarrow\left(d_1;d_2\right)=45^0\)
Đúng 0
Bình luận (0)
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.