xét dấu biểu thức
(-x) (x-3)3/5x+10
Xét dấu các biểu thức: a) f(x)=( 4 - x ) × ( 5x - 10 ) b) f(x)=x × (1/3 × x - 1)
xét dấu các biểu thức sau
a. f(X)=11X+3/-x2+5x-7
\(f\left(x\right)=\dfrac{11x+3}{-x^2+5x-7}.\)
Ta có: \(-x^2+5x-7\) là 1 tam thức bậc 2.
\(\left\{{}\begin{matrix}a=-1< 0.\\\Delta=5^2-4.\left(-1\right).\left(-7\right)=-3< 0.\end{matrix}\right.\)
\(\Rightarrow-x^2+5x-7>0\forall x\in R.\)
\(\Rightarrow\) \(f\left(x\right)>0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)< 0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)=0.\Leftrightarrow x=\dfrac{-3}{11}.\)
bài 1 giải các bất phương trình sau
a, -x2 +5x-6 ≥ 0
b, x2-12x +36≤0
c, -2x2 +4x-2≤0
d, x2 -2|x-3| +3x ≥ 0
e, x-|x+3| -10 ≤0
bài 2 xét dấu các biểu thức sau
a,<-x2+x-1> <6x2 -5x+1>
b, x2-x-2/ -x2+3x+4
c, x2-5x +2
d, x-< x2-x+6 /-x2 +3x+4 >
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
Xét dấu của các biểu thức sau :
f(x) = ( -x2+x-1)(6x2-5x+1)
A. f(x) > 0 khi và chỉ khi x ∈ 1 3 ; 1 2
B. f(x) < 0 khi và chỉ khi x ∈ 1 3 ; 1 2
C. f(x)>0 khi và chỉ khi x ∈ - ∞ ; 1 3 ∪ 1 2 ; + ∞
D. f(x)< 0 khi và chỉ khi x ∈ - ∞ ; 1 3
Chọn A
Ta có –x2+x-1= 0 vô nghiệm,
6x2- 5x+1= 0 khi x= ½ hoặc x= 1/3
Bảng xét dấu
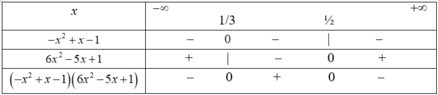
Suy ra f(x) > 0 khi và chỉ khi 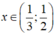
Và f( x)< 0 khi và chỉ khi 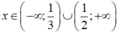
Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)
. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1
Xét dấu biểu thức: f(x) = (-3x - 3)(x + 2)(x + 3)
Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2 có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu :

Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.
xét dấu biểu thức sau : f(x) = (x2 + 3x - 2)(- x2 - 5x - 4)
Xét dấu biểu thức f(x) = (2x – 1)(-x + 3)

Các nghiệm này chia khoảng thành ba khoảng, trong mỗi khoảng các nhị thức đã cho có dấu hoàn toàn xác định.

Từ bảng xét dấu ta thấy:
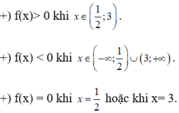
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 92: Giải bất phương trình x3 – 4x < 0.
Lời giải
x3 – 4x < 0 ⇔ x(x2 - 4) < 0 ⇔ x(x - 2)(x + 2) < 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có tập nghiệm của bất phương trình là:
S = (-∞;2) ∪ (0;2)