Xét ΔABO vuông tại B và ΔACO vuông tại C có

OA chung

\(\widehat{BOA}=\widehat{COA}\)

Do đó: ΔABO=ΔACO
Suy ra: AB=AC
hay ΔABC cân tại A

mà \(\widehat{CAB}=180^0-120^0=60^0\)

nên ΔABC đều

Bài này mình biết làm nhưng không biết vẽ hình trên máy tính

mk k cần vẽ hình, chỉ cần giải thôi

Ta có hình vẽ:

Δ OBA vuông tại B có: A₁ + O₁ = 90^o (1)

Δ OCA vuông tại C có: A₂ + O₂ = 90^o (2)

Từ (1) và (2) lại có: O₁ = O₂ vì OA là phân giác của BOC

=> A₁ = A₂

Xét Δ OBA và Δ OCA có:

A₁ = A₂ (cmt)

OA là cạnh chung

O₁ = O₂ (cmt)

Do đó, Δ OBA = Δ OCA (c.g.c)

=> AB = AC (2 cạnh tương ứng)

=> Δ ABC là tam giác cân tại A

Ta có:tam giác OBA vuông tại B

Suy ra:góc BAO+AOB=90 độ

Lại có:tam giác OCA vuông tại C

Suy ra:góc CAO+AOC=90 độ

Mà góc AOB=AOC

Suy ra:góc BAO=góc CAO

xÉT tam giác ABO và tam giác ACO theo trường hợp cạnh huyền-góc nhon.

Suy ra:AB=AC(hai cạnh tương ứng)

Suy ra:tam giác ABC là tam giác cân do AB=AC

C1 :

Hình : tự vẽ 

a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C

                                       mà CI vuông góc vs AB => CI là đường cao của tam giác ABC 

=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )

=> IA=IB (đpcm)

C1 : 

b) Có IA=IB ( cm phần a ) 

mà IA+IB = AB 

      IA + IA = 12 (cm)

=> IA = \(\frac{12}{2}=6\left(cm\right)\)

Xét tam giác vuông CIA có :     CI²  +   IA²  = CA²  ( Đ/l Py-ta -go )

                                                   CI² +  6²     = 10²

                                                          CI²       = 10²  - 6² = 64

=> CI = \(\sqrt{64}=8\left(cm\right)\)

Vậy CI ( hay IC ) = 8cm

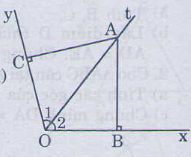
Hai tam giác vuông ACO và ABO có:

=(gt)

AO chung

Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)

Suy ra AC=AB.

Vây ∆ABC là tam giác cân(AB=AC).

Hình thím tự vẽ:

(tại cái bài lúc nãy đang làm gần xong cái tự nhiên "Ôi hỏng!!")

Gọi M là giao điểm của OA và BC

-Xét tam giác OAB và tam giác OAC có:

\(\widehat{AOB}\)=\(\widehat{AOC}\) (GT)

OA: cạnh chung

\(\widehat{B}\)=\(\widehat{C}\)=90⁰ (GT)

=> tam giác OAB = tam giác OAC

(theo trường hợp cạnh huyền góc nhọn)

Ta có: OA là phân giác góc O

\(\widehat{AOB}\)=\(\widehat{AOC}\) = \(\frac{1}{2}\)\(\widehat{O}\) = \(\frac{1}{2}\)120⁰ = 60⁰

Trong tam giác OAB có:

\(\widehat{O}\)+\(\widehat{A}\)+\(\widehat{B}\)=180⁰ (tổng 3 góc trong tam giác)

hay 60⁰ + góc A + 90⁰ = 180⁰

=> \(\widehat{A}\) = 30⁰

Vì tam giác OAB = tam giác OAC

nên \(\widehat{OAB}\)=\(\widehat{OAC}\)=30⁰

-Xét tam giác ABM và tam giác ACM có:

AM: cạnh chung

\(\widehat{BAM}\)=\(\widehat{CAM}\) (tam giác OAB = tam giác OAC)

AB = AC (tam giác OAB = tam giác OAC)

=> tam giác ABM = tam giác ACM (c.g.c)

=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)

Mà \(\widehat{AMB}\)+\(\widehat{AMC}\) = 180⁰ (kề bù)

=> \(\widehat{AMB}\)=\(\widehat{AMC}\)=90⁰

Trong tam giác ABM có:

\(\widehat{BAM}\)+\(\widehat{ABM}\)+\(\widehat{AMB}\)=180⁰ (tổng 3 góc của tam giác)

hay 30⁰ + góc ABM + 90⁰ = 180⁰

=> \(\widehat{ABM}\)=60⁰

Vì tam giác ABM = tam giác ACM

nên \(\widehat{ABM}\)=\(\widehat{ACM}\)=60⁰ (2 góc tương ứng)

Ta có: \(\widehat{BAM}\)+\(\widehat{CAM}\)=30⁰+30⁰=60⁰

Trong tam giác ABC có:

\(\widehat{BAC}\)=\(\widehat{ABC}\)=\(\widehat{ACB}\)=60⁰

=> tam giác ABC là tam giác đều

Vậy tam giác ABC là tam giác đều

"Sorry, hôm nay tớ bực bội wa"

\(\Delta BOA\)vuông tại B có: BOA + OAB = 90^o

\(\Delta COA\)vuông tại C có: COA + OAC = 90^o

Mà BOA = COA vì OA là tia phân giác của BOC

=> OAB = OAC

Xét \(\Delta BOA\) và \(\Delta COA\) có:

BOA = COA (cmt)

OA là cạnh chung

BAO = CAO (cmt)

Do đó, \(\Delta BOA=\Delta COA\left(c.g.c\right)\)

=> AB = AC (2 cạnh tương ứng)

Như vậy tam giac ABC cân tại A