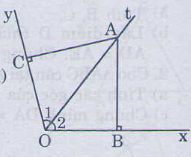
Hai tam giác vuông ACO và ABO có:
ˆO1O1^=ˆO2O2^(gt)
AO chung
Nên suy ra ∆ACO=∆ABO(cạnh huyền góc nhọn)
Suy ra AC=AB.
Vây ∆ABC là tam giác cân(AB=AC).
Cho góc xOy có số đo 120 độ , điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ AC vuông góc với Oy (C thuộc Oy). Tam giác ABC là tam giác gì ? Vì sao ?
Cho góc xOy có số đo bằng 120o , điểm A thuộc tia phân giác của góc xOy . Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ Ax vuông góc với Oy (C thuộc Oy), tam giác ABC là tam giác gì ? Vì sao ?
Cho góc xOy có số đo bằng 120 độ có Oz là tia phân giác. Trên Oz lấy điểm A, qua A vẽ AB vuông góc với Ox (B thuộc Oz), vẽ AC vuông góc với Oy (C thuộc Oy). Chứng minh rằng tam giác ABC là một tam giác đều
Cho góc xOy < 90 độ, kẻ N thuộc Ox; M thuộc Oy sao cho OM=ON.Kẻ MH, NK lần lượt vuông góc Oy, Ox.Gọi I là giao NK và MH
b, Tam giác MIN cân
c,Ss: IK và IN
Cho tam giác ABC cân ở A. Kẻ BD vuông góc AC, CE vuông góc với AB (D thuộc AC, e thuộc AB ). Gọi I là giao điểm của BD và CE. Chứng minh :
a) BE=CD
b) AI là tia phân giác của góc BAC
Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):
a, Chứng minh tam giác ABM= tam giác ACM
b, Chứng minh M là trung điểm của BC và AM vuông góc BC
c, Kẻ ME vuông góc AB ( E thuộc AB ) và MF vuông góc AC ( F thuộc AC ). Chứng minh ME=MF
Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):
a, Chứng minh tam giác ABM= tam giác ACM
b, Chứng minh M là trung điểm của BC và AM vuông góc BC
c, Kẻ MF vuông góc AB ( F thuộc AB ) và ME vuông góc AC ( E thuộc AC ). Chứng minh EF // BC
Cho tam giác ABC. Kẻ BE vuông góc với AC, kẻ CF vuông góc với AB( E thuộc AC, F thuộc AB). Gọi O là giao điểm của BE, CF. Biết OC=AB. Tính góc ACB
tam giác ABC cân ở A, M thuộc BC, kẻ MD vuông góc với AB (D thuộc AB) Kẻ ME vuông góc với AC (E thuộc AC) Kẻ BH vuông góc với AC, H thuộc AC. C/M: MD+ME=BH
