Question

Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):

a, Chứng minh tam giác ABM= tam giác ACM

b, Chứng minh M là trung điểm của BC và AM vuông góc BC

c, Kẻ ME vuông góc AB ( E thuộc  AB ) và MF vuông góc AC ( F thuộc AC ). Chứng minh ME=MF

Answer 1

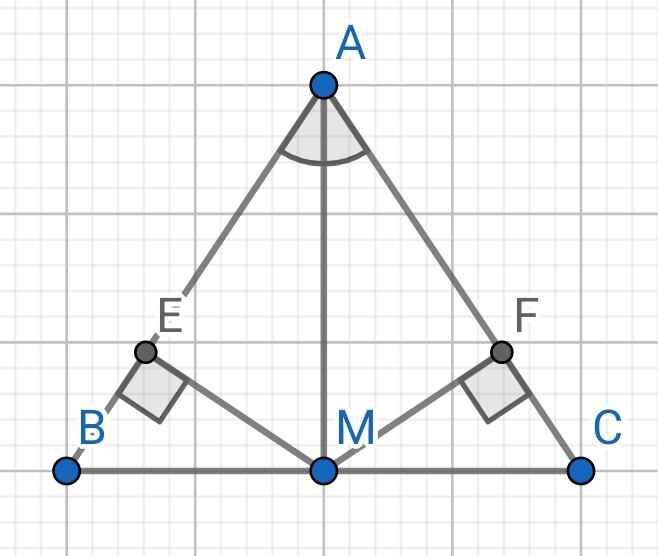
 a) Do AM là tia phân giác của ∠BAC (gt)

⇒ ∠BAM = ∠CAM

Xét ∆ABM và ∆ACM có:

AB = AC (gt)

∠BAM = ∠CAM (cmt)

AM là cạnh chung

⇒ ∆ABM = ∆ACM (c-g-c)

b) Do ∆ABM = ∆ACM (cmt)

⇒ BM = CM (hai cạnh tương ứng)

⇒ M là trung điểm của BC

Do ∆ABM = ∆ACM (cmt)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180⁰ (kề bù)

⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BC

c) Do ∠BAM = ∠CAM (cmt)

⇒ ∠EAM = ∠FAM

Xét hai tam giác vuông: ∆AME và ∆AMF có:

AM là cạnh chung

∠EAM = ∠FAM (cmt)

⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)

⇒ ME = MF (hai cạnh tương ứng)

Answer 2

a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)

b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)

c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)