sin25x-cos23x+1=0

Những câu hỏi liên quan
Số nghiệm thuộc
0
;
π
của phương trình sinx+
1
+
cos
x
2(
cos
2
3
x
+
1
)
là: A. 1. B. 2. C. 3. D. 4
Đọc tiếp
Số nghiệm thuộc 0 ; π của phương trình sinx+ 1 + cos x =2( cos 2 3 x + 1 ) là:
A. 1.
B. 2.
C. 3.
D. 4
Giải các phương trình cos 2 x + cos 2 2 x - cos 2 3 x - cos 2 4 x = 0
Giải pt ( đưa về pt bậc 2 )
cos23x - 5sin3x + 5 = 0
\(1-sin^23x-5sin3x+5=0\)
\(\Leftrightarrow-sin^23x-5sin3x+6=0\)
\(\Rightarrow\left[{}\begin{matrix}sin3x=1\\sin3x=-6< -1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow3x=\dfrac{\pi}{2}+k2\pi\)
\(\Rightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\)
Đúng 1
Bình luận (0)
Tìm m để phương trình
cos
4
x
cos
2
3
x
+
m
sin
2
x
có nghiệm
x
∈
0
;
π
12
.
Đọc tiếp
Tìm m để phương trình cos 4 x = cos 2 3 x + m sin 2 x có nghiệm x ∈ 0 ; π 12 .
![]()
![]()
![]()
![]()

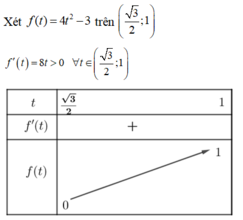
Dựa vào bảng biến thiên phương trình có nghiệm khi 0<m<1
Chọn D
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình:
cos
4
x
cos
2
3
x
+
m
sin
2
x
có nghiệm
x
∈
0
;
π
12
. A.
m
∈
0
;...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình: cos 4 x = cos 2 3 x + m sin 2 x có nghiệm x ∈ 0 ; π 12 .
A. m ∈ 0 ; 1 2 .
B. m ∈ 1 2 ; 2 .
C. m ∈ 0 ; 1 .
Đáp án C
Ta có: cos 2 3 x 1 + cos 6 x 2 = 4 cos 3 2 x − 3 cos 2 x + 1 2 và cos 4 x = 2 cos 2 2 x − 1
Khi đó, phương trình đã cho
⇔ 2 cos 2 2 x − 1 = 4 cos 3 2 x − 3 cos 2 x + 1 2 + 1 − cos 2 x 2 m
⇔ 4 cos 2 2 x − 2 = 4 cos 3 2 x − 3 cos 2 x + 1 + 1 − cos 2 x m
⇔ cos 2 x − 1 m = 4 cos 3 2 x − 4 cos 2 2 x − 3 cos 2 x + 3
Đặt t = cos 2 x , với x ∈ 0 ; π 12 → t ∈ 3 2 ; 1 do đó: * ⇔ m 4 t 3 − 4 t 2 − 3 t + 3 t − 1 = 4 t 2 − 3
Xét hàm số f t = 4 t 2 − 3 trên khoảng 3 2 ; 1 → min f t = 0 max f t = 1
Vậy để phương trình m = f t có nghiệm khi và chỉ khi m ∈ 0 ; 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình:
cos
4
x
cos
2
3
x
+
m
sin
2
x
có nghiệm
x
∈
0
;
π
12
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình: cos 4 x = cos 2 3 x + m sin 2 x có nghiệm x ∈ 0 ; π 12
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị của tham số m để phương trình:
cos
4
x
c
os
2
3
x
+
m
sin
2
x
có nghiệm
x
∈
0
;
π
12
A.
m
∈
0
;
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình: cos 4 x = c os 2 3 x + m sin 2 x có nghiệm x ∈ 0 ; π 12
A. m ∈ 0 ; 1 2
B. m ∈ 1 2 ; 2
C. m ∈ 0 ; 1
D. m ∈ − 1 ; 1 4
Đáp án C
Ta có c os 2 3 x = 1 + c os 6 x 2 = 4 c os 3 2 x − 3 c os 2 x + 1 2
và c os 4 x = 2 c os 2 2 x − 1
Khi đó, phương trình đã cho
⇔ 2 c os 2 2 x − 1 = 4 c os 3 2 x − 3 c os 2 x + 1 2 + 1 − c os 2 x 2 m
⇔ 4 c os 2 2 x − 2 = 4 c os 3 2 x − 3 c os 2 x + 1 + 1 − c os 2 x m ⇔ c os 2 x − 1 m = 4 c os 3 2 x − 4 c os 2 2 x − 3 c os 2 x + 3
Đặt t = c os 2 x , với x ∈ 0 ; π 12 → t ∈ 3 2 ; 1 ,
do đó (*) ⇔ m = 4 t 3 − 4 t 2 − 3 t + 3 t − 1 = 4 t 2 − 3.
Xét hàm số f t = 4 t 2 − 3 trên khoảng 3 2 ; 1 → min f t = 0 max f t = 1 .
Vậy để phương trình m = f t có nghiệm khi và chỉ khi m ∈ 0 ; 1 .
Đúng 0
Bình luận (0)
sin23x-cos24x=sin25x-cos26x
\(\Leftrightarrow1-cos6x-1-cos8x=1-cos10x-1-cos12x\)
\(\Leftrightarrow cos10x+cos12x-cos6x-cos8x=0\)
\(\Leftrightarrow cos11x.cosx+cos7x.cosx=0\)
\(\Leftrightarrow cosx\left(cos11x+cos7x\right)=0\)
\(\Leftrightarrow cosx.cos9x.cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cos2x=0\\cos9x=0\end{matrix}\right.\) \(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
cos
4
x
cos
2
3
x
+
m
.
sin
2
x
có nghiệm
x
∈
0
,
π
12
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình cos 4 x = cos 2 3 x + m . sin 2 x có nghiệm x ∈ 0 , π 12
![]()
![]()




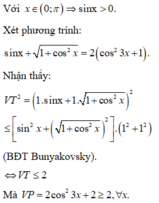




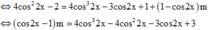
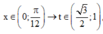 , do đó (*)
, do đó (*) 


