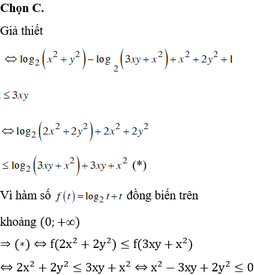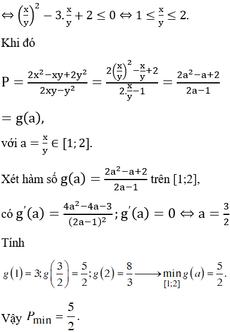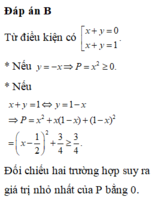Ta có : \(x^2+y^2=4< =>x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)

\(< =>4\ge\frac{\left(x+y\right)^2}{2}< =>\left(x+y\right)^2\le4.2=8< =>x+y\le\sqrt{8}\)

Hay \(x+y\le\sqrt{8}\)

Dấu = xảy ra khi và chỉ khi \(x=y=\sqrt{2}\)

Vậy GTLN của P = \(\sqrt{8}\)đạt được khi và chỉ khi \(x=y=\sqrt{2}\)

Áp dụng BĐT cói cho 2 số ko âm ta có 

X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12 

Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y 

( thông cảm mình gõ mũ ko đc ) 

\(x^2+y^2+xy=3\)

Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)

\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\) 

Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)

mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)

=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1

maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)

Đặt \(P=x^2+y^2-xy\)

\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)

\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)

\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)

\(P_{min}=1\) khi \(x=y=1\)

\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)

\(\Rightarrow P\le9\)

\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)

Đáp án D

Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0   (*)

Đặt x + y = u x y = v  ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0  gải ra ta được  u = v + 2 + v 2 + 28 v + 4 4

Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18  , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18  ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0  với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 )  trong đó t 0 = m i n t = m i n ( x y + y x )  với x,y thỏa mãn điều kiện (*).

Ta có :

t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2

Vậy  m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4

Không nhìn thấy bất cứ chữ nào của đề bài cả 

Chọn đáp án A

Ta có:

  P = 1 x ( 1 z 2 + 1 y 2 ) + 1 y ( 1 z 2 + 1 x 2 ) + 1 z ( 1 x 2 + 1 y 2 )

Đặt:  1 x = a ; 1 y = b ; 1 z = c  thì a,b,c>0 và a²+b²+c²=1

P = a b 2 + c 2 + b c 2 + a 2 + c a 2 + b 2 = a 2 a ( 1 − a 2 ) + b 2 b ( 1 − b 2 ) + c 2 c ( 1 − c 2 )

Áp dụng bất đẳng thức Côsi cho 3 số dương ta có:

a 2 1 - a 2 2 = 1 2 .2 a 2 ( 1 − a 2 ) ( 1 − a 2 ) ≤ 1 2 2 a 2 + 1 − a 2 + 1 − a 2 3 = 4 27 = > a ( 1 − a 2 ) ≤ 2 3 3 < = > a 2 a ( 1 − a 2 ) ≥ 3 3 2 a 2 ( 1 )

Tương tự:  b 2 b ( 1 − b 2 ) ≥ 3 3 2 b 2 ( 2 ) ; c 2 c ( 1 − c 2 ) ≥ 3 3 2 c 2 ( 3 )

Từ (1); (2); (3) ta có  P ≥ 3 3 2 ( a 2 + b 2 + c 2 ) = 3 3 2

Đẳng thức xảy ra  a = b = c = 1 3 h a y   x = y = z = 3

Vậy giá trị nhỏ nhất của P là  3 3 2