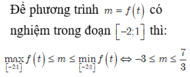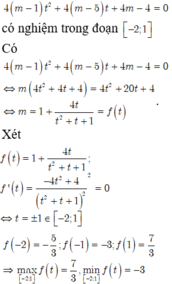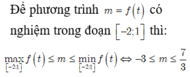Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình \(\left\{{}\begin{matrix}3\left(x-6\right)< -3\\\frac{5x+m}{2}>7\end{matrix}\right.\) có nghiệm

Những câu hỏi liên quan
Cho bất phương trình
x
4
+
x
2
+
m
3
-
2
x
2
+
1...
Đọc tiếp
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m . Tìm tất cả các giá trị thực của tham số m để bất phương trình trên nghiệm đúng ∀ x > 1 .
![]()
![]()

![]()
Tìm tất cả các giá trị nguyên của tham số m để phương trình:
\(mx^2-\left(1-2m\right)x+m-2=0^{\left(1\right)}\) có nghiệm là số hữu tỉ
(1-2m)2 - 4m(m-2) >0
1-4m +4m2-4m2 +8m >0
4m +1 >0
m > -1/4
Đúng 0
Bình luận (0)
với m> -4 thì đa thức co nghiệm là số hữu tỷ, không lẽ bn học trg chuyên mà không hiểu?
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị nguyên của tham số m để phương trình:
\(mx^2-\left(1-2m\right)x+m-2=0^{\left(1\right)}\) có nghiệm là số hữu tỉ
Tập tất cả các giá trị của tham số m để hệ bất phương trình
2
x
-
1
≥
3
x
-
m
≤
0
có nghiệm duy nhất là A.
∅
B. ...
Đọc tiếp
Tập tất cả các giá trị của tham số m để hệ bất phương trình 2 x - 1 ≥ 3 x - m ≤ 0 có nghiệm duy nhất là
A. ∅
B. 2
C. [ 2 ; + ∞ )
D. ( - ∞ ; 2 ]
Ta có 2 x - 1 ≥ 3 x - m ≤ 0 ⇔ x ≥ 2 x ≤ m . Hệ có nghiệm duy nhất khi và chỉ khi m = 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị m để bất phương trình \(\sqrt{\left(m+2\right)x+m}\ge\left|x-1\right|\)có nghiệm trên \(\left[0;2\right]\)
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn
5
4
;
4
m
-
1
+
log
1
2
2
x
-
2
2
+
4
m...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn 5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0
A. m > 7 3
B. - 3 < m < 7 3
C. - 3 ≤ m ≤ 7 3
D. m < - 3
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn
5
4
;
4
m
-
1
+
log
1
2
2
x
-
2
2
+
4
m...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn 5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0
A. m > 7 3
B. - 3 < m < 7 3
C. - 3 ≤ m ≤ 7 3
D. m < - 3
Tất cả các giá trị của tham số m để hệ phương trình
x
-
y
m
x
2
-
x
y
-
m
-
2
0...
Đọc tiếp
Tất cả các giá trị của tham số m để hệ phương trình x - y = m x 2 - x y - m - 2 = 0 có nghiệm là
A. m = 0
B. m ≠ 0
C. m = 2
D. m ≠ 2
x - y = m ( 1 ) x 2 - x y - m - 2 = 0 ( 2 )
Từ (1), ta có y = x - m , thế vào (2) ta được phương trình:
x2 – x (x- m) – m - 2= 0 ⇔ x2 – x2 + mx –m –2 = 0
hay mx –m -2 = 0 (*) .
Hệ phương trình đã cho có nghiệm khi phương trình (*) có nghiệm ⇔ m ≠ 0 .
Chọn B.
Đúng 0
Bình luận (0)
Cho hệ phương trình:
\(\hept{\begin{cases}\left(m+1\right)\cdot x+m\cdot y=2\cdot m-1\\m\cdot x-y=m^2-2\end{cases}}\)
Tìm các giá trị của m để hệ phương trình có nghiệm thoả mãn x*y lớn nhất.