cho tam giác abc vuông tại a khẳng định nào sau đây là đúng

 A b+a=90 B a+c=90 C b+c=90 Db+c=180

a, b, c, đúng còn d, sai nhé

a/sai

b/đúng

c/đúng

d/sai

Ta có A B → = 2 ; 2 ,     B C → = 0 ; −   4  và  A C → = 2 ; −   2 .

Suy ra A B = A C = 2 2 A B 2 + A C 2 = B C 2 .  

Vậy tam giác ABC vuông cân tại A.

 Chọn D

Theo định lí sin trong tam giác ta có:  a sin A = 2 R ⇒ a = 2 R . sin A

Tương tự, b = 2RsinB; c= 2R.sin C

Theo đầu bài:

 a + b =2c ⇒ 2Rsin A + 2Rsin B = 4Rsin C ⇒ sin A + sin B = 2sin C.

ĐÁP ÁN C

Ta có:   b . cos C + c . cos B = b . a 2 + b 2 − c 2 2 a b + c . c 2 + a 2 − b 2 2 a c

= a 2 + ​ b 2 − c 2 2 a + ​ c 2 + a 2 − b 2 2 a = a 2 + ​ b 2 − c 2 + c 2 + a 2 − b 2 ​ 2 a = 2 a 2 2 a = a

ĐÁP ÁN B

* Diện tích tam giác ABC là:   S ​ =    1 2 b c . sin A ⇒ 4 S = 2 b c sin A

cot A = cosA sin A = b 2 + ​ c 2 − a 2 2 b c sin A = b 2 + ​ c 2 − a 2 2 b c . s i n A = b 2 + ​ c 2 − a 2 4 S

* Tương tự, ta có:   cot B = a 2 + ​ c 2 − b 2 4 S ;     cot C = a 2 + ​ b 2 − c 2 4 S

* Do đó,

cot A + ​ cot B + cot C = b 2 + ​ c 2 − a 2 4 S + ​ a 2 + ​ c 2 − b 2 4 S + a 2 + ​ b 2 − c 2 4 S = a 2 + ​ b 2 + c 2 4 S

ĐÁP ÁN B

A. \(\sin A = \sin \,(B + C)\)

Ta có: \((\widehat A  + \widehat C) + \widehat B= {180^o}\)

\(\Rightarrow \sin \,(B + C) = \sin A\)

=> A đúng.

B. \(\cos A = \cos \,(B + C)\)

Sai vì \(\cos \,(B + C) =  - \cos A\)

C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.

Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)

Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)

D. \(\sin A\,\, \le 0\)

Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)

\( \Rightarrow \sin A > 0\)

=> D sai.

Chọn A

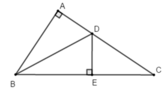
Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E

Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:

BD cạnh huyền chung

A B D ^ = E B D ^ (BD là tia phân giác của góc B)

Khi đó: Δ A B D = Δ E B D (cạnh huyền góc nhọn)

Suy ra: AD = DE (hai cạnh tương ứng) (1)

Lại có tam giác DEC vuông tại E có DC là cạnh huyền

Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)

Từ (1) và (2) suy ra DC > AD hay AD < DC

Vậy A đúng, B, C, D sai.

Chọn đáp án A