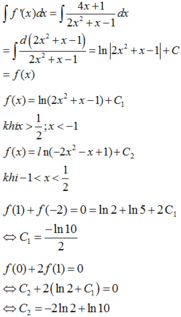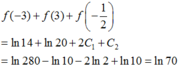Cho f(x) thỏa mãn f(1)=1,f(2)=3,f(n)+f(x+2)=2f(n+1) Tính f(1)+f(2)+...+f(2019)

Những câu hỏi liên quan
cho hàm số f(x) thỏa mãn f(1)=1,f(2)=3,f(n)+f(n+2)=2*f(n+1) với mọi số nguyên dương n.tính f(1)+f(2)+...+f(2019)
cho hàm số f(x) thỏa mãn f(1)=1,f(2)=3,f(n)+f(n+2)=2*f(n+1) với mọi số nguyên dương n.tính f(1)+f(2)+...+f(2019)
Cho hàm số f thỏa mãn: f(1)=1; f(2)=3;f(n)+f(n+2)=2f(n+1) với mọi số nguyên dương n. Vậy f(1)+f(2)+...+f(30) bằng
Cho đa thức f(x) thỏa mãn f(x)+2f(3/2x^2-1/2x-1)=x^3-x+3 với mọi x.Chứng minh rằng f(1)+f(-1)=2f(0)
Cho hàm số \(f\) xác định trên \(ℕ^∗\) và thỏa mãn:
\(f\left(n+1\right)=n\left(-1\right)^{n+1}-2f\left(n\right)\) và \(f\left(1\right)=f\left(2024\right)\)
Tính \(S=f\left(1\right)+f\left(2\right)+f\left(3\right)...+f\left(2023\right)\)
cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(1/3)
hàm số f(x) xác định với mọi x thỏa mãn \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)nên:
+) x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=\frac{1}{9}\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=\frac{2}{9}\)(1)
+) x = \(\frac{1}{3}\)thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=9\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{-79}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{-79}{27}\)
Làm ngược, sửa:))
+) Nếu x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=9\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(1)
+) Nếu x = \(\frac{1}{3}\) thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{161}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{7}\)
cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(2019)
\(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\) (1)
\(\Rightarrow f\left(\frac{1}{x}\right)+2f\left(x\right)=\frac{1}{x^2}\Rightarrow2f\left(\frac{1}{x}\right)+4f\left(x\right)=\frac{2}{x^2}\) (2)
Trừ (2) cho (1): \(3f\left(x\right)=\frac{2}{x^2}-x^2\Rightarrow f\left(x\right)=\frac{2}{3x^2}-\frac{1}{3}x^2\)
\(\Rightarrow f\left(2019\right)=\frac{2}{3.2019^2}-\frac{1}{3}.2019^2\)
Cho hàm số f(x) xác định trên R{-1;1/2} và thỏa mãn
f
x
4
x
+
1
2
x
2
+
x
-
1
;
f
1
+
f
-
2
0...
Đọc tiếp
Cho hàm số f(x) xác định trên R\{-1;1/2} và thỏa mãn f ' x = 4 x + 1 2 x 2 + x - 1 ; f 1 + f - 2 = 0 và f(0) + 2f(1)=0. Giá trị của biểu thức f(-3) + f(-3) + f(-1/2) bằng:
A. ln14+ln20-3/2ln10
B. -ln10
C.ln70
D. ln28
Cho hàm số f(x) thỏa mãn
∫
0
1
(
x
+
1
)
f
(
x
)
d
x
10
và 2f(1) – f(0) 2. Tính I
∫
0
1
f
(
x
)
d
x
A. I -12. B. I 8. C. I 12. D. I -8.
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) – f(0) = 2. Tính I = ∫ 0 1 f ( x ) d x
A. I = -12.
B. I = 8.
C. I = 12.
D. I = -8.
Chọn D.
Đặt u = x + 1 d v = f ' ( x ) d x ⇒ d u = d x v = ∫ f ' ( x ) d x
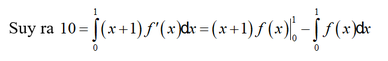
⇔ 10 = 2f(1) – f(0) – I ⇔ 10 = 2 – I ⇔ I = -8.
Đúng 0
Bình luận (0)