a) Chia cả 2 vế cho 2 ta được : \(x=\dfrac{\sqrt{13}}{2}\approx1,803\)

b) Chia cả 2 vế cho -5 ta được : \(x=\dfrac{1+\sqrt{5}}{-5}\approx-0,647\)

c) Chia cả 2 vế cho \(\sqrt{2}\) ta được: \(x=\dfrac{4\sqrt{3}}{\sqrt{2}}\approx4,889\)

a)2x=\(\sqrt{13}\)

<=>x=\(\dfrac{\sqrt{13}}{2}\)

<=>x=1,803

b, -5x = 1 + \(\sqrt{5}\)

<=>x=\(\dfrac{1+\sqrt{5}}{-5}\)

<=>x= -0,647

\(\left[{}\begin{matrix}x=2\sqrt{2}\simeq2.82\\x=-2\sqrt{2}\simeq-2.82\end{matrix}\right.\)

Ta có: a = 1,414…; b = 2,236

Làm tròn đến chữ số thập phân thứ nhất, ta được: \(a \approx 1,4;b \approx 2,2\)

Tổng 2 số thập phân nhận được là: 1,4 + 2,2 = 3,6

a) Ta có: 

√4(1+6x+9x2)24(1+6x+9x2)2 =√4.√(1+6x+9x2)2=4.(1+6x+9x2)2

                                   =√4.√(1+2.3x+32.x2)2=4.(1+2.3x+32.x2)2

                                   =√22.√[12+2.3x+(3x)2]2=22.[12+2.3x+(3x)2]2

                                   =2.√[(1+3x)2]2=2.[(1+3x)2]2

                                   =2.∣∣(1+3x)2∣∣=2.|(1+3x)2|

                                   =2(1+3x)2=2(1+3x)2.

 (Vì  (1+3x)2>0(1+3x)2>0 với mọi xx  nên ∣∣(1+3x)2∣∣=(1+3x)2|(1+3x)2|=(1+3x)2)

Thay x=−√2x=−2 vào biểu thức rút gọn trên, ta được: 

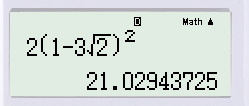
                                2[1+3.(−√2)]2=2(1−3√2)22[1+3.(−2)]2=2(1−32)2.

Bấm máy tính, ta được: 2(1−3√2)2≈21,0292(1−32)2≈21,029.

b) Ta có:

√9a2(b2+4−4b)=√32.a2.(b2−4b+4)9a2(b2+4−4b)=32.a2.(b2−4b+4)

                                  =√(3a)2.(b2−2.b.2+22)=(3a)2.(b2−2.b.2+22)

                                  =√(3a)2.√(b−2)2=(3a)2.(b−2)2

                                  =|3a|.|b−2|=|3a|.|b−2|

Thay a=−2a=−2 và b=−√3b=−3 vào biểu thức rút gọn trên, ta được:

|3.(−2)|.∣∣−√3−2∣∣=|−6|.∣∣−(√3+2)∣∣|3.(−2)|.|−3−2|=|−6|.|−(3+2)|

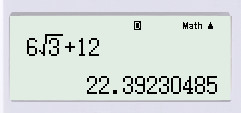
                                     =6.(√3+2)=6√3+12=6.(3+2)=63+12.

Bấm máy tính, ta được: 6√3+12≈22,39263+12≈22,392. 

a) Ta có: 

$\sqrt{4(1+6x+9x^2{)}^2}=\sqrt{4}.\sqrt{(1+6x+9x^2{)}^2}$

                                       $=\sqrt{4}.\sqrt{(1+2.3x+3^2.x^2{)}^2}$

                                       $=\sqrt{2^2}.\sqrt{[1^2+2.3x+(3x{)}^2{]}^2}$

                                       $=2.\sqrt{\left[\right(1+3x{)}^2{]}^2}$

                                       $=2.|(1+3x{)}^2|$

                                       $=2(1+3x{)}^2$.

 (Vì  $(1+3x{)}^2\ge 0$ với mọi $x$ nên $|(1+3x{)}^2|=(1+3x{)}^2$)

Thay $x=-\sqrt{2}$ vào biểu thức rút gọn trên, ta được: 

$2[1+3.(-\sqrt{2}){]}^2=2(1-3\sqrt{2}{)}^2$.

Bấm máy tính, ta được: $2(1-3\sqrt{2}{)}^2$ $\approx$ $21,029$.

b) Ta có:

$\sqrt{9a^2(b^2+4-4b)}=\sqrt{3^2.a^2.(b^2-4b+4)}$

                                      $=\sqrt{(3a{)}^2.(b^2-2.b.2+2^2)}$

                                      $=\sqrt{(3a{)}^2.(b-2{)}^2}$

                                      $=\sqrt{(3a{)}^2}.\sqrt{(b-2{)}^2}$

                                      $=|3a|.|b-2|$

Thay $a=-2$ và $b=-\sqrt{3}$ vào biểu thức rút gọn trên, ta được:

$|3.(-2)|.|-\sqrt{3}-2|=|-6|.|-\sqrt{3}-2|$

                                     $=6.(\sqrt{3}+2)=6\sqrt{3}+12$.

Bấm máy tính, ta được: $6\sqrt{3}+12$ $\approx$ $22,392$.

a) x = 21 , 029

b) x = 22 , 392

??????????????????????????????????????

??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????

Chắc bạn ghi nhầm căn thức thứ 2

\(A2\sqrt{2}=2\sqrt{\left(2x+4\right)\left(x^2-2x+4\right)}+2\sqrt{\left(2y+4\right)\left(y^2-2y+4\right)}+2\sqrt{\left(2z+4\right)\left(z^2-2z+4\right)}\)

\(A2\sqrt{2}\le2x+4+x^2-2x+4+2y+4+y^2-2y+4+2z+4+z^2-2z+4\)

\(A2\sqrt{2}\le x^2+y^2+z^2+24=72\)

\(A\le18\sqrt{2}\)

Dấu "=" xảy ra khi \(x=y=z=4\)