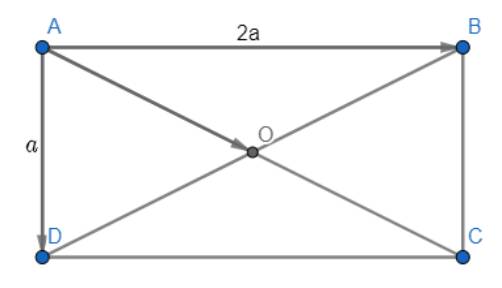
Cho hình chữ nhật ABCD có tâm o cạnh AB = 2a và AD = a. Tính / AB + AD / và / BC - OD /
có ai giúp mình làm bài này với
Cho hình chữ nhật ABCD có tâm O và AB= a AD =2a . Dựng và tính độ dài các véc tơ
1) 2AO - BC
2) OC + 2AB
3) 3AB + 2OD
Lời giải:
1.
$\overrightarrow{2AO}-\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AB}$
Độ dài: $|\overrightarrow{AB}|=a$
2.
Trên tia đối của $AC$ lấy $T$ sao cho $TA=OC$
Trên tia đối của $BA$ lấy $K$ sao cho $BA=BK$
$\overrightarrow{OC}+2\overrightarrow{AB}=\overrightarrow{TA}+\overrightarrow{AB}+\overrightarrow{AB}$
$=\overrightarrow{TB}+\overrightarrow{AB}$
$=\overrightarrow{TB}+\overrightarrow{BK}=\overrightarrow{TK}$
Ta có:
$TC=3OC=\frac{3}{2}AC=\frac{3}{2}\sqrt{(2a)^2+a^2}=\frac{3\sqrt{5}}{2}a$
$CK=\sqrt{BC^2+BK^2}=\sqrt{(2a)^2+a^2}=\sqrt{5}a$
$\cos \widehat{TCK}=\cos 2\widehat{TCB}=2\cos^2 \widehat{TCB}-1$
$=2(\frac{CB}{AC})^2-1=\frac{3}{5}$
Áp dụng định lý cos:
$TK^2=TC^2+CK^2-2TC.CK\cos \widehat{TCK}$
$=\frac{45}{4}a^2+5a^2-9a^2=\frac{29}{4}a^2$
$\Rightarrow TK=\frac{\sqrt{29}}{2}a$
3. Trên tia đối tia $CD$ lấy $M$ sao cho $CM=CD$
$3\overrightarrow{AB}+2\overrightarrow{OD}=3\overrightarrow{DC}+2\overrightarrow{OD}=2\overrightarrow{OC}+\overrightarrow{DC}$
$=\overrightarrow{AC}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AM}$
$AM=\sqrt{AD^2+DM^2}=\sqrt{(2a)^2+(2a)^2}=2\sqrt{2}a$
Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:
a) \(\overrightarrow {AB} .\overrightarrow {AO} \);
b) \(\overrightarrow {AB} .\overrightarrow {AD} \).
a) \(AC = BD = \sqrt {A{B^2} + A{D^2}} \\= \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5 \)
\(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \cos \widehat {OAB} =\\ \cos \widehat {CAB} = \frac{{AB}}{{AC}} = \frac{{2a}}{{a\sqrt 5 }} = \frac{{2\sqrt 5 }}{5}\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AO} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AO} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) \\= AB.\frac{1}{2}AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right)\\ = 2a.\frac{1}{2}.a\sqrt 5 .\frac{{2\sqrt 5 }}{5} = 2{a^2}\end{array}\)
b) \(AB \bot AD \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = 90^o \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) =0 \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
Cho hình chữ nhật ABCD có tâm O. Biết 5 , 12 . AB a AD a a. Chứng minh rằng: AC AB OC OD b. Chứng minh rằng: AB AD BC CD
Cho hình chóp S.ABCD có các cạnh bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB=2a, AD=a. Gọi K là điểm thuộc BC sao cho 2 B K → + 2 C K → = 0 → . Tính khoảng cách giữa hai đường thẳng AD và SK.
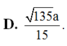
Cho hình chóp S.ABCD có các cạnh bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có A B = 2 a , A D = a . Gọi K là điểm thuộc BC sao cho 3 B K → + 2 C K → = 0 → . Tính khoảng cách giữa hai đường thẳng AD và SK.
A. 2 165 a 15 .
B. 165 a 15 .
C. 2 135 a 15 .
D. 135 a 15 .
1.Cho hình chữ nhật ABCD có AB = 4cm và BC = 3cm; trên cạnh AB lấy điểm E, nối E với D,E với C; trên cạnh AD lấy điểm G, nối G với B, G với C. Tính :
a) Diện tích hình chữ nhật ABCD.
b) Diện tích hình tam giác EDC, GDC
bài này vẽ hình nhung mình vẽ rồi các bạn giúp mình giải với
2.Cho hình tam giác có đấy BC = 6cm, chiều cao tương ứng bằng 4cm. Trên BC lấy các điểm M và N sao cho BM = MN = NC. Tính diện tích hình tam giác AMN.
bài này mình cũng ve hình rồi ác bạn giúp mình giải với mình cảm ơn nhiều
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có A B = 2 a , A D = 4 a , S A ⊥ A B C D và cạnh SC tạo với đáy góc 60 ° . Gọi M là trung điểm của BC, N là điểm trên cạnh AD sao cho DN = a . Khoảng cách giữa MN và SB là
A. 2 a 285 19
B. a 285 19
C. 2 a 95 19
D. 8 a 19
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a, AB = a, cạnh bên SA = a 2 và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm của cạnh BC. Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD
A. a 6 6
B. a 6 4
C. a 6 2
D. a 6 3
Đáp án C
Gọi O là trung điểm của SD. Ta có:
A D = D M = a 2 và A D = 2 a ⇒ A M ⊥ D M
Lại có D M ⊥ S A ⇒ D M ⊥ S A M ⇒ D M ⊥ S M
Vì tam giác SAD vuông tại A nên OS = OD = OA. Tương tự với tam giác SMD nên OS = OD = OM.
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ADM. Khi đó R = S D 2 = S A 2 + D A 2 2 = a 6 2 .
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=a , AD=2a Cạnh bên SA vuông góc với đáy (ABCD), SA=2a Tính tan của góc giữa hai ămtj phẳng (SBD) và (ABCD)
A. 1 5
B. 2 5
C. 5
D. 5 2