Các bn giúp mik câu này vs
Giải hệ phương trình x^4-2y=y^4-2z=z^4-2x=-0.5
Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^5=x^4-2x^2y+2\\y^5=y^4-2y^2z+2\\z^5=z^4-2z^2x+2\end{matrix}\right.\)
giải hệ phương trình :
3x^2+2y+4=2z(x+3)
3y^2+2z+4=2x(y+3)
3z^2+2x+4=2y(z+3)
Giải hệ phương trình
\(\left\{{}\begin{matrix}-2x+y+z=a\\x-2y+z=b\\x+y-2z=c\end{matrix}\right.\) với x,y,z là các ẩn số
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3y=b-a\\3x-3y=2b+c\\x+y-2z=c\end{matrix}\right.\) (nhân -1 vào 2 vế pt 1 và cộng pt 2, nhân 2 vào 2 vế pt 2 và cộng pt 3)
\(\Leftrightarrow\left\{{}\begin{matrix}0=a+b+c\\x-y=\dfrac{2b+c}{3}\\x+y-2z=c\end{matrix}\right.\)
- Nếu \(a+b+c\ne0\) hệ vô nghiệm
- Nếu \(a+b+c=0\) hệ có vô số nghiệm
Giải hệ phương trình
\(\left\{{}\begin{matrix}-2x+y+z=a\\x-2y+z=b\\x+y-2z=c\end{matrix}\right.\) với x,y,z là các ẩn số
Giải các hệ phương trình :
a) \(\left\{{}\begin{matrix}x+2y-3z=2\\2x+7y+z=5\\-3x+3y-2z=-7\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}-x-3y+4z=3\\3x+4y-2z=5\\2x+y+2z=4\end{matrix}\right.\)
a) \(\left\{{}\begin{matrix}x+2y-3z=2\\2x+7y+z=5\\-3x+3y-2z=-7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x+2y-3z=2\\3y+7z=1\\-32z=-4\end{matrix}\right.\)
Đáp số : \(\left(x,y,z\right)=\left(\dfrac{55}{24},\dfrac{1}{24},\dfrac{1}{8}\right)\)
b) \(\left\{{}\begin{matrix}-x-3y+4z=3\\3x+4y-2z=5\\2x+y+2z=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x-3y+4z=3\\-5y+10z=14\\-5y+10z=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x-3y+4z=3\\-5y+10z=14\\0y+0z=-4\end{matrix}\right.\)
Phương trình cuối vô nghiệm, suy ra hệ phương trình đã cho vô nghiệm
Giải các hệ pt, bất pt sau:
a, \(\left\{{}\begin{matrix}2x-2y+z=3\\2x+y-2z=-3\\3x-4y-z=4\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}2x-3y\ge2\\3x+2y< 4\\x-2y\ge5\end{matrix}\right.\)
a: \(\left\{{}\begin{matrix}2x-2y+z=3\\2x+y-2z=-3\\3x-4y-z=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-4y+2z=6\\8x+4y-8z=-3\\3x-4y-z=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-6z=3\\11x-9z=1\\3x-4y-z=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\z=\dfrac{1}{2}\\4y=3x-z-4=\dfrac{3}{2}-\dfrac{1}{2}-4=1-4=-3\end{matrix}\right.\)
=>x=1/2;z=1/2;y=-3/4
1) {x^2+2x^2=3 {2x^2+3x^2=5 2) giải theo m {x+y=2m+1 {x-y=1 3)giải theo m {x +2y=3m+2 {2x+y=3m+2 4) cho hệ. {x+3y=4m+4 {2x+y=3m+3 Tìm m để hệ có nghiệm (x,y) thỏa mãn x+y=4 HỆ PHƯƠNG TRÌNH HẾT Ạ Giúp mik với nhé
4:
x+3y=4m+4 và 2x+y=3m+3
=>2x+6y=8m+8 và 2x+y=3m+3
=>5y=5m+5 và x+3y=4m+4
=>y=m+1 và x=4m+4-3m-3=m+1
x+y=4
=>m+1+m+1=4
=>2m+2=4
=>2m=2
=>m=1
3:
x+2y=3m+2 và 2x+y=3m+2
=>2x+4y=6m+4 và 2x+y=3m+2
=>3y=3m+2 và x+2y=3m+2
=>y=m+2/3 và x=3m+2-2m-4/3=m+2/3
3x=2y=z và x+y+z=99
2x=3y=-2z và 2x-3y+4z=48
x/0.5=y/0.3=z/0.2 và 2x+3y-4z=34
x-1/3=y-2/4=z-3/5 và x+y+z=30
x+1/3=y+2/-4=z-3/5 và 3x+2y+4z=47
x/4=y/4 và x^2y=100
giúp mình với
\(3x=2y=z\Rightarrow\frac{z}{6}=\frac{x}{2}=\frac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{z}{6}=\frac{x}{2}=\frac{y}{3}=\frac{x+y+z}{6+2+3}=\frac{99}{11}=9\)
\(\Rightarrow\hept{\begin{cases}z=54\\x=18\\y=27\end{cases}}\)
\(\frac{2x}{1}=\frac{-3y}{-1}=\frac{4z}{-2}\)
áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{2x}{1}=\frac{-3y}{-1}=\frac{4z}{-2}=\frac{2x-3y+4z}{1+-1-2}=\frac{48}{-2}=-24\)
\(\Rightarrow\hept{\begin{cases}x=-12\\y=-8\\z=-12\end{cases}}\)
\(\frac{x-1}{3}=\frac{y-2}{4}=\frac{z-3}{5}=\frac{x+y+z-6}{12}=\frac{24}{12}=2\)
\(\Leftrightarrow\hept{\begin{cases}x=7\\y=10\\z=13\end{cases}}\)
Giải các hệ phương trình x + 3 y + 2 z = 8 2 x + 2 y + z = 6 3 x + y + z = 6
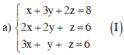
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số ta có:
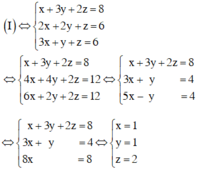
Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 2).