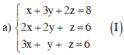
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số ta có:
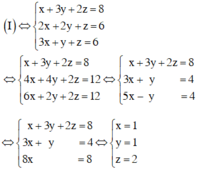
Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 2).
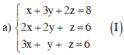
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số ta có:
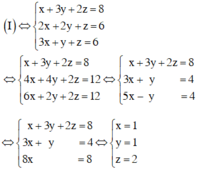
Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 2).
Hệ phương trình
2x 2z 3 0
3 8 0
3x 2 1 0
y
x y z
y z
có nghiệm là:
A. (x;y;z)=(-1;3;2) B. (x;y;z)=(1;-3;2) C. (x;y;z)=(1;-3;-2) D. (x;y;z)=(-1;3;-2)
GIẢI HỘ MÌNH VỚI, CẦN GẤP Ạ
1.Giải hệ phương trình: \(\hept{\begin{cases}\left(x+\sqrt{x^2+1}\right)\left(\sqrt{y^2+1}-y\right)=1\\3\sqrt{x+2y-2}+x\sqrt{x-2y+6}=10\end{cases}.}\)
2.cho các số thực không âm x,y,z thỏa mãn: \(x^3+y^3+z^3=3\)
Tìm Min \(P=\frac{xyz+\left(x+y+z\right)^2}{xy+yz+xz}-\frac{1}{xy+yz+xz+1}\)
Cho hệ phương trình - x + 2 y - 3 z = 2 6 x - y + 3 z = - 3 - 2 x - 3 y + z = 2
Giả sử (x; y;z) là nghiệm của hệ phương trình. Trong các khẳng định sau, khẳng định đúng là
![]()
![]()
![]()
![]()
giải hệ phương trình bằng ứng dụng tính đơn điệu của hàm số : \(\hept{\begin{cases}x^3+x^2+x+1=4y\\y^3+y^2+y+1=4z\\z^3+z^2+z+1=4x\end{cases}}\)
GIẢI HỆ PHƯƠNG TRÌNH SAU \(\hept{\begin{cases}x^3-2x=y\\y^3+2y=z\\x+y+z+1+\sqrt{x-1}=0\end{cases}}\).(CẢM ƠN CÁC BẠN)
Giải hệ phương trình:
\(\hept{\begin{cases}x+2my-z=1\\2x-my-2z=2\\x-\left(m+4\right)y-z=1\end{cases}}\)
có nghiệm (x;y;z) với m khác 0 và -4/3
Giải hệ phương trình sau(giải chi tiết)
\(\hept{\begin{cases}x+3y+2z=8\\2x+2y+z=6\\3x+y+z=6\end{cases}}\)
1, Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^3-y^3-8x=3y\\x^2-3y^2=6\end{matrix}\right.\)
1)Giải hệ phương trình với \(x,y,z\in R\)
\(\left\{{}\begin{matrix}x+\sqrt{yz}=1\\y+\sqrt{zx}=1\\z+\sqrt{xy}=1\end{matrix}\right.\)
2)Cho đa thức \(P\left(x\right)=ax^2+bx+c\) thoả mãn \(\overline{abc}\) là số nguyên tố
a)Xác định \(P\left(x\right)\) biết \(P\left(0\right)=3,P\left(1\right)=4\)
b)Chứng minh \(P\left(x\right)\) vô nghiệm trên \(Z\)
3)Tìm tất cả các hàm \(f\):\(R\rightarrow R\) thoả mãn :
\(f\left(x^2\right)=f\left(x+y\right).f\left(x-y\right)+y^2,\forall x,y\in R\)
4)Cho đường tròn \(\left(I,r\right)\) nội tiếp \(\Delta ABC\).\(M\in\) đoạn \(BC\), \(\left(M\ne B,C\right)\).Gọi \(\left(I_1,r_1\right)\)là đường tròn nội tiếp \(\Delta AMC\).Đường thẳng song song \(BC\) tiếp xúc \(\left(I_1,r_1\right)\) cắt các cạnh \(AB,AC\) tại \(X,Y\).\(AM\) cắt \(XY\) tại \(N\).Gọi \(\left(I_2,r_2\right)\) là đường tròn nội tiếp \(\Delta AXN\).Chứng minh:
a)\(A,I,I_1,I_2\) cùng thuộc 1 đường tròn
b)\(r=r_1+r_2\)