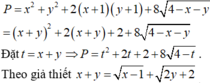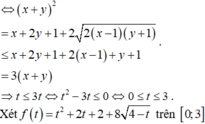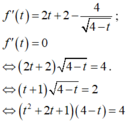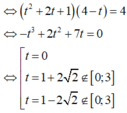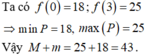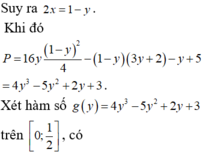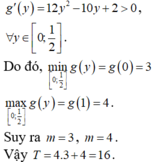Cho x,y là các số thực sao cho \(x-2y+2=2\left(\sqrt{x-1}+\sqrt{3-2y}\right)\). Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x - 2y. Tính M + m

Những câu hỏi liên quan
Cho x,y là các số thực sao cho \(x-2y+2=2\left(\sqrt{x-1}+\sqrt{3-2y}\right).\). Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x - 2y. Tính M + m
Cho x,y là các số thực sao cho \(x-2y+2=2\left(\sqrt{x-1}+\sqrt{3-2y}\right)\). Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x - 2y. Tính M + m
Xét các số thực x, y thỏa mãn
\(\sqrt{x^2+y^2+4x-2y+5}+\sqrt{x^2+y^2-8x-14y+65}=6\sqrt{2}\)
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(T=x^2+y^2-2x+2y+2\).Tính P = m + M
Ta có: \(\sqrt{x^2+y^2+4x-2y+5}+\sqrt{x^2+y^2-8x-14y+65}=6\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(x+2\right)^2+\left(y-1\right)^2}+\sqrt{\left(4-x\right)^2+\left(7-y\right)^2}=6\sqrt{2}\left(^∗\right)\)
Xét hai vectơ \(\overrightarrow{u}=\left(x+2;y-1\right)\)và \(\overrightarrow{v}=\left(4-x;7-y\right)\)
Ta có: \(\overrightarrow{u}+\overrightarrow{v}=\left(6;6\right)\Rightarrow\left|\overrightarrow{u}+\overrightarrow{v}\right|=\sqrt{6^2+6^2}=6\sqrt{2}\)
Do vậy \(\left(^∗\right)\)trở thành\(\overrightarrow{u}+\overrightarrow{v}=\left|\overrightarrow{u}+\overrightarrow{v}\right|\)
Điều này xảy ra khi và chỉ khi \(\overrightarrow{u}\)và \(\overrightarrow{v}\)cùng hướng
\(\Leftrightarrow\hept{\begin{cases}\left(x+2\right)\left(7-y\right)=\left(y-1\right)\left(4-x\right)\\\left(x+2\right)\left(4-x\right)\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=x+3\\-2\le x\le4\end{cases}}\)
Khi y = x + 3 thì \(x^2+y^2-2x+2y+2=2x^2+6x+17\)
Xét hàm số \(f\left(x\right)=2x^2+6x+17\)trên đoạn \(\left[-2;4\right]\)
Ta có: \(-\frac{6}{2.2}=\frac{-3}{2}\in\left[-2;4\right]\)và \(f\left(-2\right)=13;f\left(-\frac{3}{2}\right)=\frac{25}{2};f\left(4\right)=73\)
Suy ra \(|^{min}_{\left[-2;4\right]}f\left(x\right)=\frac{25}{2}\);\(|^{max}_{\left[-2;4\right]}f\left(x\right)=73\)
Do đó \(m=\frac{25}{2};M=73\)và \(n+M=\frac{171}{2}\)
Vậy \(n+M=\frac{171}{2}\)
cho các số thực x,y thỏa mãn \(\left\{{}\begin{matrix}\max\limits\left\{5;9x+7y-20\right\}\le x^2+y^2\le2x+8\\y\le1\end{matrix}\right.\). gọi M, m lần lượt là giá trị lớn nhất và gtnn của biểu thức P = x-2y. tính M - m
Bạn xem lại đề nghen, đoạn thỏa mãn đó có vấn đề phải không nhỉ?
Đúng 0
Bình luận (4)
Bạn nên dùng Geogebra hoặc Desmos vẽ cái đường tròn kia sẽ dễ nhìn hơn, gửi nhầm vô phần cmt của bạn dưới nên mình gửi lại

Đúng 1
Bình luận (0)
Cho x, y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
x
2
+
y
2
+
2
(
x
+
1
)
(
y
+
1
)
+
8
4
-
x
-...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43
Cho x , y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
2...
Đọc tiếp
Cho x , y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y . Khi đó, giá trị của M+m bằng.
A. 41
B. 42
C. 43
D. 44
Cho hai số thực x, y thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
11
−
2
x
−
y
2
y...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Đáp án C
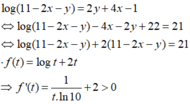
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
và
log
11
-
2
x
-
y
2
y
+
4
x
-
1
. Xét biểu thức
P
16
x...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 và log 11 - 2 x - y = 2 y + 4 x - 1 . Xét biểu thức P = 16 x 2 y - 2 x 3 y + 2 - y + 5 . Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
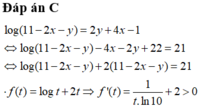
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
2
, và
log
(
11
-
2
x
-
y
)
2...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 2 , và log ( 11 - 2 x - y ) = 2 y + 4 x - 1 . Xét biểu thức P = 16 y x 2 - 2 x ( 3 y + 2 ) - y + 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của T = ( 4 m + M ) bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19