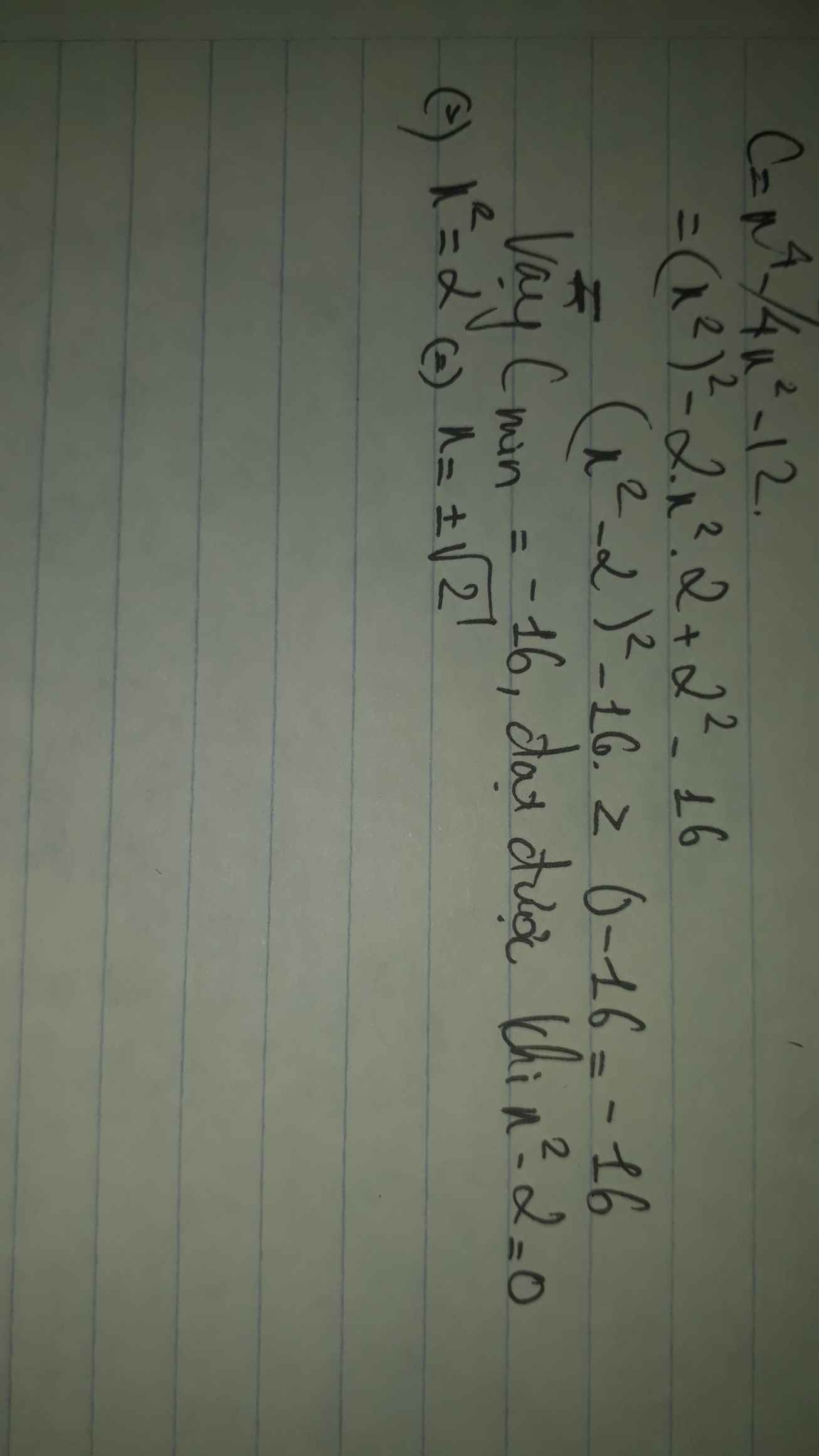A= 4x⁴+4x²+12

Vì 4x⁴;4x² \(\ge0\)

=> A=4x⁴+4x²+12 \(\ge\)12

Để A nhỏ nhất => A=12

Khi đó 4x⁴+4x²+12=12

=> 4x⁴+4x²=0

=> x=0

Vậy giá trị nhỏ nhất của A=12 khi x=0 

\(A=2x^2+4x+1=2\left(x^2+2x+1\right)-1=2\left(x+1\right)^2-1\ge-1\)

\(A_{min}=-1\) khi \(x=-1\)

Câu B chỉ có max, ko có min

\(B=-x^2+3x+4=-\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{25}{4}=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)

\(B_{max}=\dfrac{25}{4}\) khi \(x=\dfrac{3}{2}\)

Câu C cũng chỉ có max, không có min

\(C=-4x^2+8x=-4\left(x^2-2x+1\right)+4=-4\left(x-1\right)^2+4\le4\)

\(C_{max}=4\) khi \(x=1\)

Câu D cũng chỉ có max, không có min

\(D=\dfrac{3}{4x^2-4x+1+4}=\dfrac{3}{\left(2x-1\right)^2+4}\le\dfrac{3}{4}\)

\(C_{max}=\dfrac{3}{4}\) khi \(x=\dfrac{1}{2}\)

(4 câu có 3 câu sai đề)

a)

\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)

Daaus = xayr ra khi: x = 2

b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)

Dấu = xảy ra khi x = 3

c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)

Dấu = xảy ra khi

2x = y và y = 2

=> x = 1 và y = 2

a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)

Dấu "=" <=> x = 2

b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)

Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)

c) \(4x^2+2y^2-4xy-4y+1\)

= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)

= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)

Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

E=\(\left(4x^4+4x^2+1\right)-5\)

=\(\left(2x^2+1\right)^2-5\)

ta thấy \(\left(2x^2+1\right)^2\)>hoặc bằng 0 với mọi x

=>\(\left(2x^2+1\right)^2-5\)>hoặc bằng -5 với mọi x

Dấu "=" xảy ra khi 2x²+1=0<=>2x²=-1(vô lí)

VẬY ........................................

\(E=4x^4+4x^2-4\)

\(E=\left(2x^2\right)^2+4x^2+1-5\)

\(E=\left(2x^2+1\right)^2-5\)

             Vì \(2x^2\ge0\Rightarrow2x^2+1\ge1\)

                        \(\Rightarrow\left(2x^2+1\right)^2-5\ge-4\)

Dấu = xảy ra khi \(2x^2=0\Rightarrow x=0\)

           Vậy Min A = -4 khi x = 0

\(4x^2+2x+12\)

\(=\left(4x^2+2x+\frac{1}{4}\right)+\frac{47}{4}\)

\(=\left[\left(2x\right)^2+2.\frac{1}{2}\left(2x\right)+\left(\frac{1}{2}\right)^2\right]+\frac{47}{4}\)

\(=\left(2x+\frac{1}{2}\right)^2+\frac{47}{4}\)

Có :

\(\left(2x+\frac{1}{2}\right)^2\ge0\)với mọi \(x\)

\(\Rightarrow\left(2x+\frac{1}{2}\right)^2+\frac{47}{4}\ge\frac{47}{4}\)

\(\Rightarrow\text{​​}\)GTNN của \(4x^2+2x+12\)là \(\frac{47}{4}\)

Đẳng thức xảy ra khi :

\(2x+\frac{1}{2}=0\)

\(2x=-\frac{1}{2}\)

\(x=-\frac{1}{4}\)

Vậy GTNN của \(4x^2+2x+12=\frac{47}{4}\)khi \(x=-\frac{1}{4}.\)

Ta có C=x^2-4x-4 / x^2-4x+5

            =x^2-4x+4-8/x^2-4x+4+1

            =(x^2-4x+4)-8 / (x^2-4x+4)+1

            =(x-2)^2 -8/ (x-2)^2 +1

            =Vì (x-2)^2 >hoặc = 0

          =>(x-2)^2-8 > hoặc = -8 và (x-2)^2+1> hoặc =1  (với mọi x)

         Dấu ''='' xảy ra   <=> (x-2)^2 =0

                                   <=>x - 2 = 0

                                   <=>x      =2 

            <=> Giá trị nhỏ nhất của biểu thức C là  -8/1=-8

 Vậy giá trị nhỏ nhất của biểu thức C là  minC= - 8  khi x=2

              Chúc bạn làm bài tốt !  Mình ko chắc câu trả  lời của mình đúng đâu  , nhưng cũng ko phải là sai