Lời giải:
$x^2-2y^2=5\Rightarrow x$ lẻ. Đặt $x=2k+1$ với $k$ nguyên 

$x^2-2y^2=5$

$\Leftrightarrow (2k+1)^2-2y^2=5$

$\Leftrightarrow 2k^2+2k-y^2=2$

$\Rightarrow y$ chẵn. Đặt $y=2t$ với $t$ nguyên

PT trở thành: $2k^2+2k-4t^2=2$
$\Leftrightarrow k^2+k-2t^2=1$

Điều này vô lý do $k^2+k-2t^2=k(k+1)-2t^2$ chẵn còn $1$ thì lẻ

Vậy pt vô nghiệm.

        4x²+4x=8y³-2z+4

<=> 2x²+2x=4y³-z+2

<=>2x(x+1)=4y³-2z+2

Ta có : VT chia hết cho 4 =>VP chia hết cho 4 , 4y³ chia hết cho 4 

                                                                      2z chia hết cho 4 => z chia hết cho 2 , mà 2 ko chia hết cho 2 => pt trên không có No nguyên

Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).

Vậy pt vô nghiệm nguyên.

2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).

Lời giải:

PT $\Leftrightarrow x^2+x(3y-1)+(2y^2-2)=0$

Coi đây là pt bậc 2 ẩn $x$ thì:

$\Delta=(3y-1)^2-4(2y^2-2)=y^2-6y+9=(y-3)^2$. Do đó pt có 2 nghiệm:

$x_1=\frac{1-3y+y-3}{2}=-y-1$

$x_2=\frac{1-3y+3-y}{2}=2-2y$

Đến đây bạn thay vô pt ban đầu để giải pt bậc 2 một ẩn thui.

ai giúp em bài1 và phần b bài 2 với ạ

ai giup vs 

Cho x,y là hai số thoả mãn 2(x²+y²)=(x-y)² Khi đó ta có hệ thức biểu diễn mối quan hệ giữa x,y là   x=....y
giải chi tiết nha

đáp án là 43 ai thông minh sẽ tick câu trả lời này

Đáp án: D

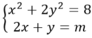
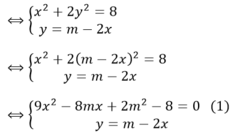
Để hệ phương trình có nghiệm thì phương trình (1) có nghiệm, tức là:

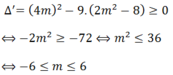
Vậy giá trị lớn nhất của m để hệ phương trình có nghiệm là 6.

Ta có  2 x + y = 5 m − 1 x − 2 y = 2

⇔ y = 5 m − 1 − 2 x x − 2 5 m − 1 − 2 x = 2 ⇔ y = 5 m − 1 − 2 x 5 x = 10 m

⇔ x = 2 m y = m − 1

Thay vào x 2   –   2 y 2   =   − 2 ta có

x 2 – 2 y 2 = − 2 ⇔ ( 2 m 2 ) – 2 ( m − 1 ) 2   = − 2 ⇔ 2 m 2 + 4 m = 0 ⇔ m = 0 m = − 2    

Vậy m ∈ {−2; 0}

Đáp án: C