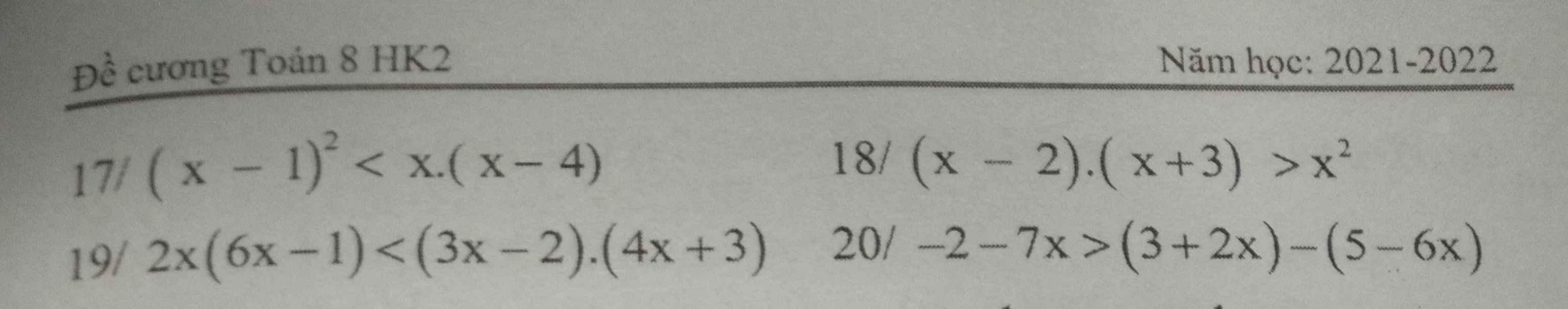Question

CMR phương trình sau không có nghiệm nguyên

x²=2y²-8y+3

Answer 1

\(x^2=2\left(y-2\right)^2-5\)

Do vế phải lẻ \(\Rightarrow\) vế trái lẻ \(\Rightarrow x=2k+1\)

\(\Rightarrow\left(2k+1\right)^2=2y^2-8y+3\)

\(\Leftrightarrow2k^2+2k-2=y^2-4y\)

\(\Leftrightarrow2k\left(k+1\right)+4y-2=y^2\)

Do \(k\left(k+1\right)⋮2\) \(\forall k\Rightarrow2k\left(k+1\right)+4y⋮4\)

\(\Rightarrow\) Vế trái chia hết cho 2 nhưng ko chia hết cho 4 nên ko thể là SCP

Vậy pt ko có nghiệm nguyên