xác định k để x2+8x+k=0 biết hiệu cuả chúng 2 nghiệm là 1

Những câu hỏi liên quan
XÁC ĐỊNH K ĐỂ PHƯƠNG TRÌNH x2 + 2x + k =0 có hai nghiệm thỏa mãn 1/x1 + 1/x2 =1/4
Lời giải:
Để pt có 2 nghiệm thì: $\Delta'=1-k\geq 0\Leftrightarrow k\leq 1$
Áp dụng định lý Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=-2$
$x_1x_2=k$
$x_1,x_2\neq 0\Leftrightarrow x_1x_2\neq 0\Leftrightarrow k\neq 0$
Khi đó:
$\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{4}$
$\Leftrightarrow \frac{x_1+x_2}{x_1x_2}=\frac{1}{4}$
$\Leftrightarrow \frac{-2}{k}=\frac{1}{4}\Leftrightarrow k=-8$ (tm)
Đúng 1
Bình luận (0)
Cho phương trình : x2 - 4mx +9(m-1)2 0a. Xem xét với các giá trị nào của m thì phương trình trên có nghiệm ?b. Giả sử x1, x2 là nghiệm của phương trình đã cho, hãy tính tổng và tích của chúng. Tìm một hệ thức giữa x1 và x2 không phụ thuộc vào m.c. Xác định giá trị của m để hiệu các nghiệm của phương trình bằng 4.
Đọc tiếp
Cho phương trình : x2 - 4mx +9(m-1)2 = 0
a. Xem xét với các giá trị nào của m thì phương trình trên có nghiệm ?
b. Giả sử x1, x2 là nghiệm của phương trình đã cho, hãy tính tổng và tích của chúng. Tìm một hệ thức giữa x1 và x2 không phụ thuộc vào m.
c. Xác định giá trị của m để hiệu các nghiệm của phương trình bằng 4.
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
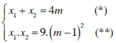
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
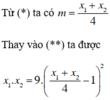
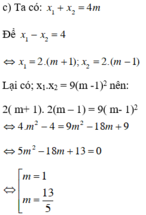
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành 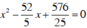 có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
Đúng 0
Bình luận (0)
Xác định k để phương trình: (k-1)x^2+2(k+1)x+k=0
có hai nghiệm dương
Giải thích nè : 1 ) a khác 0 vì phương trình bậc thì a phải khác 0 , nên a = 0 thì sẽ biến thành pt bậc nhất .
2 ) S > 0 ( S là tổng 2 nghiệm ) ; Vì tổng của 2 số dương phải lớn hơn 0 ( vd : 1 + 2 = 3 ; 0 + 6 = 6 )
3 ) \(P\ge0\) ( P là tích của 2 nghiệm ) ; Vì tích của 2 số dương phải lớn hơn hoặc bằng 0 ( vd : 4 . 5 = 20 ; 0 . 243 = 0 )
4 ) \(\Delta'>0\) vì đenta phẩy > 0 thì phương trình mới có 2 nghiệm phân biệt \(x_1;x_2\)
Ta có : ( a = k - 1 ; b = 2(k+ 1 ) ; b' = k + 1 ; c = k )
Pt có 2 nghiệm dương \(\Leftrightarrow\hept{\begin{cases}a\ne0\\S>0;P\ge0\\\Delta'>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a\ne0\\-\frac{b}{a}>0;\frac{c}{a}\ge0\\b^{'^2}-ac>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}k-1\ne0\\\frac{-2\left(k+1\right)}{k-1}>0;\frac{k}{k-1}\ge0\\\left(k+1\right)^2-\left(k-1\right).k>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}k\ne1\\-2k-2>0;k-1>0;k\ge0;k-1\ge0\\k^2+2k+1-k^2+k>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}k\ne1\\k< -1;k>1;k\ge0;k\ge1\\3k+1>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}k\ne1\\k< -1;k>1\\k>-\frac{1}{3}\end{cases}}\) ( Vì k > 1 và \(k\ge0\) nên ta chỉ lấy k > 1 thôi ; và loại bỏ \(k\ge1\) vì k phải khác 1 )
\(\Leftrightarrow\hept{\begin{cases}k\ne1\\k< -1\\k>1\end{cases}}\) ( loại bỏ k > -1/3 vì ta đã có k > 1 rồi nên không cần phải có k > -1/3 nữa )
Ta có : k < -1 có nghĩa là \(\left(-\infty;-1\right)\) trừ vô cùng đến trừ 1
: k > 1 có nghĩa là \(\left(1;+\infty\right)\) 1 đến cộng vô cùng
Lấy 2 tập hợp này giao lại với nhau :
Vậy đây là một tập hợp rỗng \(\left(\varnothing\right)\)
Vậy nên k không thể xác định được .
Học tốt !
Đúng 0
Bình luận (0)
cho pt 8x^2 - 8x + m^2 + 1 = 0
a) định m để pt có nghiệm x = 1/2
b) định m để pt có 2 nghiệm thỏa dk : x1^4 - x2^4 = x1^3 - x2^3
1. Xác định k sao cho pt: k^2x^2- (k+1)x -5 =0 có hai nghiệm trái dấu
2. Cho pt: x^2 -8x +14 =0 ko giải pt hãy tính:
a, Tổng các nghịch đảo của các nghiệm.
b, Tổng các bình phương của các nghiệm.
c, Tổng các lập phương của các nghiệm.
cho các phương trình
x2-5x+k=0 và x2-7x+2k=0
xác định k để 1 trong các ngiệm của pt (2) lớn gấp 2 lần một trong các nghiệm của pt (1).
Lời giải:
Để pt $(1)$ và $(2)$ có nghiệm thì \(\left\{\begin{matrix} \Delta(1)=25-4k\geq 0\\ \Delta(2)=49-8k\geq 0\end{matrix}\right.\Leftrightarrow k\leq \frac{49}{8}\)
Gọi $t$ là nghiệm $(1)$ thì yêu cầu đề bài được xử lý khi $2t$ là nghiệm của $(2)$
\(\Leftrightarrow \left\{\begin{matrix} t^2-5t+k=0\\ (2t)^2-14t+2k=0\end{matrix}\right.\)
\(\Rightarrow 2(t^2-5t)-4t^2+14t=0\)
$\Leftrightarrow t=0$ hoặc $t=2$.
Nếu $t=0$ thì hiển nhiên loại
Nếu $t=2$ thì $k=6$.
Thử lại thấy thỏa mãn.
Đúng 2
Bình luận (0)
Định k để phương trình:
x
2
+
4
x
2
−
4
x
−
2
x
+
k
−
1
0
có đúng hai nghiệm lớn hơn 1. A. k -8 B. -8 k 1 C. 0 k 1 D. Không tồn tại k
Đọc tiếp
Định k để phương trình: x 2 + 4 x 2 − 4 x − 2 x + k − 1 = 0 có đúng hai nghiệm lớn hơn 1.
A. k < -8
B. -8 < k < 1
C. 0 < k < 1
D. Không tồn tại k
Ta có: x 2 + 4 x 2 − 4 x − 2 x + k − 1 = 0
⇔ x − 2 x 2 − 4 x − 2 x + k + 3 = 0 ( 1 )
Đặt t = x − 2 x h a y x 2 − t x − 2 = 0 , phương trình trở thành t 2 − 4 t + k + 3 = 0 (2)
Nhận xét: với mỗi nghiệm t của phương trình (2) cho ta hai nghiệm trái dấu của phương trình (1)
Ta có :
∆ ' = 4 - k + 3 = 1 - k ⇒ phương trình (2) có hai nghiệm phân biệt t 1 = 2 − 1 − k , t 2 = 2 + 1 − k với k < 1
+ Với t 1 = 2 − 1 − k thì phương trình x 2 − 2 − 1 − k x − 2 = 0 có 1 nghiệm
x > 1 ⇔ a f ( 1 ) < 0 ⇔ 1 2 − 2 − 1 − k .1 − 2 < 0 ⇔ k > − 8
+ Với t 2 = 2 + 1 − k thì phương trình x 2 − 2 + 1 − k x − 2 = 0 có 1 nghiệm
x > 1 ⇔ a f ( 1 ) < 0 ⇔ 1 2 − 2 + 1 − k .1 − 2 < 0 ⇔ − 3 − 1 − k < 0 (luôn đúng với k < 1 )
Vậy kết hợp điều kiện k < 1 ta được - 8 < k < 1
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho pt (m+1)x2-2(m-1)x+m-20a, Xác định m để pt có 2 nghiệm phân biệtb, Xác định m để pt có một nghiệm bằng 2. Tìm nghiệm kiac, Xác định m để pt có 2 nghiệm x1; x2 thỏa mãn 1/x1 + 1/x2 7/4; 1/x1 + 1/x2 1; x12+x222d, Xác định m để pt có 2 nghiệm thỏa mãn 3(x1+x2)5x1x2
Đọc tiếp
Cho pt (m+1)x2-2(m-1)x+m-2=0
a, Xác định m để pt có 2 nghiệm phân biệt
b, Xác định m để pt có một nghiệm bằng 2. Tìm nghiệm kia
c, Xác định m để pt có 2 nghiệm x1; x2 thỏa mãn 1/x1 + 1/x2 = 7/4; 1/x1 + 1/x2 = 1; x12+x22=2
d, Xác định m để pt có 2 nghiệm thỏa mãn 3(x1+x2)=5x1x2
Cho hai phương trình
x
2
−
13
x
+
2
m
0
(
1
)
v
à
x
2
−
4
x
+
m
0
(
2
)
. Xác định m để một nghiệm phương trình (1) gấp đôi một nghiệm phương trình (2) A. −45 B. −5 C. 0 và −5 D. Đáp án khác
Đọc tiếp
Cho hai phương trình x 2 − 13 x + 2 m = 0 ( 1 ) v à x 2 − 4 x + m = 0 ( 2 ) . Xác định m để một nghiệm phương trình (1) gấp đôi một nghiệm phương trình (2)
A. −45
B. −5
C. 0 và −5
D. Đáp án khác
Gọi nghiệm của phương trình (2) là x0 (x0 ≠ 0)
thì nghiệm phương trình (1) là 2x0
Thay x0; 2x0 lần lượt vào phương trình (2) và (1)
ta được
2 x 0 2 − 13.2 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0
⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0 ⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 4 x 0 2 − 16 x 0 + 4 m = 0
⇔ 10x0 = −2m ⇔ x 0 = − m 5
Do x0 ≠ 0 nên m ≠ 0
Thay x 0 = − m 5 vào phương trình (2)
ta được − m 5 2 − 4. − m 5 + m = 0
⇔ m 2 25 + 4 m 5 + m = 0
⇔ m 2 25 + 9 m 5 = 0 ⇒ m = 0 m = − 45
Kết hợp m ≠ 0 ta được m = −45
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)











