chứng minh phần đảo của định lí mê nê la uýt

Cho tam giác ABC, AM là trung tuyến. Lấy I thuộc AM sao cho AI = 4IM. Gọi P là giao điểm của BI và AC. CMR: AP=2PC
hình như câu này áp dụng định lí Mê-nê-la-uýt
ace nào thấy thì giúp em vs ạ
thanks nhiều
đảo mê la nê đi và đảo ?
A . lục địa B. san hô C. chuỗi đảo san hô D . đảo núi lửa , chuỗi đảo núi lửa
câu hỏi phải là : đảo mê la nê đi là đảo :
câu trả lời D
Ở châu Đại Dương khí hậu ôn đới phân bố chủ yếu ở
A. quần đảo Niu Di-len và phía bắc Ô-xtrây-li-a.
B. quần đảo Niu Di-len và phía nam Ô-xtrây-li-a.
C. quần đảo Niu Di-len và chuỗi đảo Mê-la-nê-di.
D. quần đảo Niu Di-len và chuỗi đảo Pô-li-nê-di.
Ở châu Đại Dương khí hậu ôn đới phân bố chủ yếu ở
A. quần đảo Niu Di-len và phía bắc Ô-xtrây-li-a.
B. quần đảo Niu Di-len và phía nam Ô-xtrây-li-a.
C. quần đảo Niu Di-len và chuỗi đảo Mê-la-nê-di.
D. quần đảo Niu Di-len và chuỗi đảo Pô-li-nê-di.
châu đại dương gồm lục địa Ô-Xtrây-li-a và
A.quần đảo Niu Di -len B.chuỗi đảo san hô ,núi lưa mê -la -nê -di
C.vô số đảo và quần đảo D.chuỗi đảo san hô bô-li-ne -di
GIÚP MÌNH VỚI Ạ
lục địa ô xtraya lia có những dạng địahình nào?
a.cao nguyên đb núi
b.sơn nguyên đb núi
c.đồng bằng núi đồi
d.núi đồi cao nguyên
ha oai thuoocj quần đảo nào?
a. mê la nê di
b.niu di len
c. micro nê di
d.pô li nê di
đúng cho nhanh nhứt;-;
Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
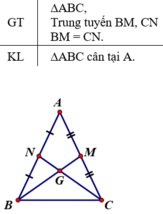
Giả sử ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G.
⇒ G là trọng tâm của tam giác
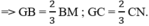
Mà BM = CN (theo gt) ⇒ GB = GC ⇒ GM = GN.
Xét ΔGNB và ΔGMC có :
GN = GM (cmt)
GB = GC (cmt)
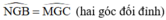
⇒ ΔGNB = ΔGMC (c.g.c) ⇒ NB = MC.
Lại có AB = 2.BN, AC = 2.CM (do M, N là trung điểm AC, AB)
⇒ AB = AC ⇒ ΔABC cân tại A.
Hãy chứng minh định lí đảo của định lí trên : Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G => G là trọng tâm của tam giác => GB = BM; GC = CN mà BM = CN (giả thiết) nên GB = GC => ∆GBC cân tại G => do đó ∆BCN = ∆CBM vì: BC là cạnh chung CN = BM (gt) (cmt) => => ∆ABC cân tại A
Hãy chứng minh định lí đảo của định lí trên : Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
định lí đảo của định lí trên là: trong 1 tam giác cân thì 2 đường trung tuyến nối từ 2 đỉnh ở đáy bằng nhau
giả sử ta có tam giác ABC cân tại A, BD là đường trung tuyến nối từ đỉnh B tới AC( D thuộc AC); CE là đường trung tuyến nối từ đỉnh C tới AB( E thuộc AB)
suy ra B=C và
AC=AB suy ra 1/2 AB=1/2AC suy ra EA=EB=DE=DC
xét tam giác DBC và tam giác ECB có:
EB=DC(cmt)
BC(chung)
B=C(tam giác ABC cân tại A)
suy ra tam giac sDBC=ACB(c.g.c)
suy ra EC=BD
Hãy chứng minh định lí đảo của định lí trên : Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân ?
Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G
=> G là trọng tâm của tam giác
=> GB = BM; GC = CN
mà BM = CN (giả thiết) nên GB = GC
=> ∆GBC cân tại G =>
do đó ∆BCN = ∆CBM vì:
BC là cạnh chung
CN = BM (gt)
(cmt)
=> => ∆ABC cân tại A