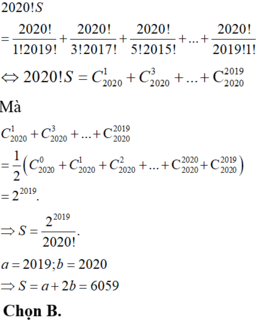Tìm số nguyên a,b biết a+2ab+2b=4

Những câu hỏi liên quan
Tìm số nguyên a;b biết a+2ab+2b=4
Trần Phúc Nguyên đề thiếu !
1, Tìm số nguyên a,b sao cho
a, a/2 + 3/b = 1/4
b, a + 2ab + 2b = 12
Tìm số nguyên a, b sao cho:
a)2ab+a+4b=5
b)6a-b+2ab=7
c)3a^2-3ab-2a=6-2b
d)2ab+a+b=2
Tìm các số nguyên a và b sao cho: \(a^2-2ab+2b^2-4a+7< 0\)
Do a và b nguyên ta cộng 1 vào vế trái của BPT đã cho và được:
a2 -2ab + 2b2 - 4a + 8 < hoặc = 0
<=> 2a2 - 4ab + 4b2 - 8a + 16 < hoặc = 0
<=> ( a-2b)2 + (a-4)2 < hoặc = 0
Dấu "=" xảy ra khi :
a=4;b=2
Tìm a,b nguyên biết: \(2a^2+2b^2+2ab-8a-8b+10=0\)
Ta có : \(2a^2+2b^2+2ab-8a-8b+10=0\)
\(\Leftrightarrow\left(a^2+2ab+b^2\right)+\left(a^2-8a+16\right)+\left(b^2-8b+16\right)=22\)
\(\Leftrightarrow\left(a+b\right)^2+\left(a-4\right)^2+\left(b-4\right)^2=22\). Dễ thấy \(\left(a+b\right)^2\le22\Rightarrow a+b< \sqrt{22}< \sqrt{16}=4\)
Phân tích : \(22=3^2+3^2+2^2\).
Từ đó chia ra các trường hợp , ta chọn được (a;b) = (1;1) ; (1;2) ; (2;1)
Đúng 0
Bình luận (0)
tìm các số nguyên a và b sao cho : a2-2ab+2b2-4a+7<0
Do a và b nguyên ta cộng 1 vào vế trái của BPT đã cho và được:
a2 -2ab + 2b2 - 4a + 8 < hoặc = 0
<=> 2a2 - 4ab + 4b2 - 8a + 16 < hoặc = 0
<=> ( a-2b)2 + (a-4)2 < hoặc = 0
Dấu "=" xảy ra khi :
a=4;b=2
Đúng 0
Bình luận (0)
Do a và b nguyên ta cộng 1 vào vế trái của BPT đã cho và được:
a2 -2ab + 2b2 - 4a + 8 < hoặc = 0
<=> 2a2 - 4ab + 4b2 - 8a + 16 < hoặc = 0
<=> ( a-2b)2 + (a-4)2 < hoặc = 0
Dấu "=" xảy ra khi :
a=4;b=2
Đúng 1
Bình luận (0)
Tìm các số nguyên a và b sao cho:
\(a^2-2ab+2b^2-4a+7< 0\)
Tìm các số tự nhiên a,b biết:
a) a . b = a + b
b) 2ab + a + 2b + 1 = 7
Biết rằng tổng
S
1
1
!
2019
!
+
1
3
!
2017
!
+
1
5
!
2015
!
+
.
.
.
+
1
2019...
Đọc tiếp
Biết rằng tổng S = 1 1 ! 2019 ! + 1 3 ! 2017 ! + 1 5 ! 2015 ! + . . . + 1 2019 ! 1 ! có thể viết dưới dạng 2 a b ! với a, b là số nguyên dương. Tính S = a + 2b
A. S = 6058
B. S = 6059
C. S = 6056
D. S = 6057