Rút gọn biểu thức sau
\(A=\sqrt{8+\sqrt{8}+\sqrt{20}+\sqrt{40}}\)
Rút gọn biểu thức sau
\(\sqrt{8+\sqrt{8}+\sqrt{20}+\sqrt{40}}\)
Rút gọn biểu thức :
\(A=\sqrt{8+\sqrt{8}+\sqrt{20}+\sqrt{40}.}\)
\(A=\sqrt{8+\sqrt{8}+\sqrt{20}+\sqrt{40}=\sqrt{\sqrt{5}^2+\sqrt{2}^2+1^2+2\sqrt{2}.1}+2\sqrt{5}.1+2\sqrt{2}\sqrt{5}}\)
=\(\sqrt{\left(\sqrt{5}+\sqrt{2}+1\right)^2=\sqrt{5}+\sqrt{2}+1}\)
Rút gọn biểu thức
\(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}-3\sqrt{5\sqrt{48}}}\)
\(2\sqrt{5\sqrt{3}}-2\sqrt{8\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
Help me plsssssss
Help me plssssssss
a: \(=2\sqrt{20\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\cdot\sqrt{20\sqrt{3}}\)
\(=4\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}=-4\sqrt{5\sqrt{3}}\)
b: \(=2\sqrt{5\sqrt{3}}-4\sqrt{2\sqrt{3}}-6\sqrt{5\sqrt{3}}=-4\sqrt{5\sqrt{3}}-4\sqrt{2\sqrt{3}}\)
Rút gọn các biểu thức sau:
a.\(2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
b.\(\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\)
c.\(\sqrt{8+\sqrt{40}+\sqrt{20}+\sqrt{8}}\)
d.\(\sqrt{10+\sqrt{24}+\sqrt{20}+\sqrt{8}}\)
d.\(\sqrt{10+\sqrt{24}-\sqrt{40}-\sqrt{60}}\)
a/ \(\sqrt{2}+\sqrt{6}\)
b/ Sửa đề:
\(\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}=1\)
c/ \(1+\sqrt{2}+\sqrt{5}\)
a/ \(2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
\(=2\sqrt{3+\sqrt{5-\sqrt{12+2.2\sqrt{3}+1}}}\)
\(=2\sqrt{3+\sqrt{5-\sqrt{\left(2\sqrt{3}+1\right)^2}}}\)
\(=2\sqrt{3+\sqrt{5-\left(2\sqrt{3}+1\right)}}\)
\(=2\sqrt{3+\sqrt{4-2\sqrt{3}}}\)
\(=2\sqrt{3+\sqrt{3-2\sqrt{3}+1}}\)
\(=2\sqrt{3+\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=2\sqrt{3+\left(\sqrt{3}-1\right)}\)
\(=\sqrt{2}\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{2}\sqrt{3+2\sqrt{3}+1}\)
\(=\sqrt{2}\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=\sqrt{2}\left(\sqrt{3}+1\right)\)
\(=\sqrt{2}+\sqrt{6}\)
Rút gọn biểu thức: B = \(\sqrt{5}\left(\sqrt{20}-\sqrt{8}\right)+2\sqrt{10}\)
\(B=\sqrt{5}\left(\sqrt{20}-\sqrt{8}\right)+2\sqrt{10}\)
\(=\sqrt{100}-\sqrt{40}+2\sqrt{10}\)
\(=\sqrt{10^2}-\sqrt{2^2.10}+2\sqrt{10}\)
\(=10-2\sqrt{10}+2\sqrt{10}\)
\(=10+0\)
\(=10\)
Rút gọn biểu thức :
a) \(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
b) \(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
a) \(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
\(=2\sqrt{40.2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{5.4\sqrt{3}}\)
\(=\left(2\sqrt{80}-2\sqrt{5}-3\sqrt{20}\right).\sqrt{\sqrt{3}}\)
\(=\left(8\sqrt{5}-2\sqrt{5}-6\sqrt{5}\right).\sqrt{\sqrt{3}}=0\)
b) \(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
\(=\left(4\sqrt{2}-2\sqrt{5}-6\sqrt{5}\right).\sqrt{\sqrt{3}}\)
\(=\left(4\sqrt{2}-8\sqrt{5}\right).\sqrt{\sqrt{3}}\)
\(=\sqrt{\sqrt{3}}\left(\sqrt{2}-2\sqrt{5}\right)\)
a)2\(\sqrt{40\sqrt{12}}\) -2\(\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
=\(2\sqrt{40.2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
=\(2\sqrt{80\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
=\(8\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}\)
=0
b)\(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
=\(4\sqrt{2\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}\)
=4\(\sqrt{2\sqrt{3}}-8\sqrt{5\sqrt{3}}\)
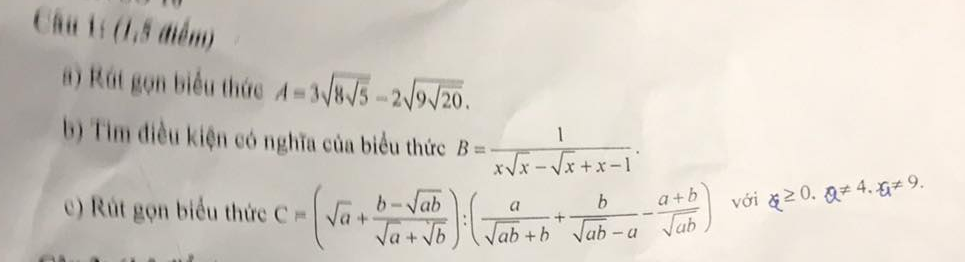
c1
a. rút gọn biểu thức
\(A=3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\)
b. tìm đk có nghĩa của biểu thức
\(B=\dfrac{1}{x\sqrt{x}-\sqrt{x}+x-1}\)
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
Rút gọn các biểu thức sau :
a) A= \(\sqrt{18}\) . \(\sqrt{2}\) - \(\sqrt{48}\) : \(\sqrt{3}\)
b)B= \(\dfrac{8}{\sqrt{5}-1}\) + \(\dfrac{8}{\sqrt{5}+1}\)
a) \(A=\sqrt{18}.\sqrt{2}-\sqrt{48}:\sqrt{3}=\sqrt{18.2}-\sqrt{48:3}\)
\(=\sqrt{36}-\sqrt{16}=6-4=2\)
b) \(B=\dfrac{8}{\sqrt{5}-1}+\dfrac{8}{\sqrt{5}+1}=\dfrac{8\sqrt{5}+8+8\sqrt{5}-8}{\left(\sqrt{5}-1\right).\left(\sqrt{5}+1\right)}=\dfrac{16\sqrt{5}}{4}=4\sqrt{5}\)
Rút gọn các biểu thức
a) \(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
b) \(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)