chứng tỏ đường thẳng -mx + 2y = m+3 luôn đi qua điểm cố định. Xác định tọa độ I

Những câu hỏi liên quan
Chứng tỏ rằng đường thẳng mx + 3 + (3m - 1)y = 0 luôn đi qua một điểm cố định với mọi m. Tìm tọa độ điểm cố định đó?
Giả sử ( x 0 ; y 0 ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.
Ta có:
m x 0 + 3 + (3m - 1) y 0 = 0 với mọi m
⇔ m x 0 + 3 + 3m y 0 - y 0 = 0 với mọi m
⇔ m( x 0 + 3 y 0 ) + 3 - y 0 = 0 với mọi m
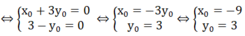
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)
Đúng 0
Bình luận (0)
Cho hàm số y = mx + (2m + 1) (1)
Với mỗi giá trị của m ∈ R, ta có một đường thẳng xác định bởi (1). Như vậy, ta có một họ đường thẳng các định bởi (1). Chứng minh rằng với mọi giá trị của m, họ đường thẳng xác định bởi (1) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm đó.
Chứng minh họ đường thẳng y = mx + (2m + 1) (1) luôn đi qua một điểm cố định nào đó.
Giả sử điểm A( x o ; y o ) là điểm mà họ đường thẳng (1) đi qua với mọi m. Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).
Với mọi m, ta có: y o = m x o + (2m + 1) ⇔ ( x o + 2)m + (1 – y) = 0
Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.
Suy ra: x o + 2 = 0 ⇔ x o = -2
1 – y o = 0 ⇔ y o = 1
Vậy A(-2; 1) là điểm cố định mà họ đường thẳng y = mx + (2m + 1) luôn đi qua với mọi giá trị m.
Đúng 0
Bình luận (0)
(P): y=\(\dfrac{x^2}{2}\) (d): y=mx+m+5
a)Chứng minh đường thẳng (d) luôn đi qua một điểm cố định với mọi giá trị m và tìm tọa độ điểm cố định đó.
b)Đường thẳng (d) luôn cắt parabol (P) tại 2 điểm phân biệt
Xem thêm câu trả lời
Cho đường thẳng
y=mx+(3m-1)
. Tọa độ điểm M cố định mà đường thẳng luôn đi qua là:
gọi điểm có tọa độ mà đường thăng y=mx+(3m-1) luôn đi qua
là \(M\left(x0,y0\right)\)
=>x0,y0 thỏa mãn y=mx+(3m-1)
\(=>y0=mx0+3m-1\)
\(< =>mx0+3m-1-y0=0\)
\(< =>m\left(x0+3\right)-\left(y0+1\right)=0\)
\(=>\left\{{}\begin{matrix}x0+3=0\\y0+1=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x0=-3\\y0=-1\end{matrix}\right.\)
vậy đường thăng y=mx+(3m-1) luôn đi qua M(-3;-1) cố định
Đúng 3
Bình luận (1)
chứng tỏ rằng đường thẳng y=mx-2(m+1) luôn đi qua 1 điểm cố định thuộc đường thẳng y=x-4
Chứng tỏ rằng họ đường thẳng (d ): y=mx+m+1 luôn đi qua 1 điểm cố định.
Gọi 2 điểm cố định là \(A\left(x_0;y_0\right)\)
Thay vào ptđt (d) ta được : \(y_0=mx_0+m+1\Leftrightarrow mx_0+m+1-y_0=0\)
\(\Leftrightarrow m\left(x_0+1\right)+\left(1-y_0\right)=0\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}x_0+1=0\\1-y_0=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=1\end{cases}}\Rightarrow A\left(-1;1\right)\)
Vậy d luôn đi qua 1 điểm cố định A(-1;1)
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình :
14.x2=x−114.x2=x−1
<=> x2 = 4x - 4
<=> x2 - 4x + 4 = 0 <=> (x - 2)2 = 0 <=> x - 2= 0 <=> x = 2
=> y = 2-1 = 1
Vậy (P) cắt (d) tại 1 điểm duy nhất là (2;1)
=> đpcm
đúng ko ?????????????
sai thì cho mik xin lỗi
cho đường thẳng D1 có phương trình : y=mx-3
D2 có phương trình : y = 2mx + 1 -m
a) Vẽ trên cùng 1 mặt phẳng tọa độ Oxy các đường thẳng D1 và D2 ứng với m =1 . Tìm tọa độ giao điểm B của chúng . Qua O viết phương trình đường thẳng vuông góc với D1 tại A
b) Chứng tỏ rằng : Đường thẳng D1 và D2 đều đi qua những điểm cố định . Tìm tọa độ điểm cố định đó
cho đường thẳng D1 có phương trình : y=mx-3
D2 có phương trình : y = 2mx + 1 -m
a) Vẽ trên cùng 1 mặt phẳng tọa độ Oxy các đường thẳng D1 và D2 ứng với m =1 . Tìm tọa độ giao điểm B của chúng . Qua O viết phương trình đường thẳng vuông góc với D1 tại A
b) Chứng tỏ rằng : Đường thẳng D1 và D2 đều đi qua những điểm cố định . Tìm tọa độ điểm cố định đó
Bài 10: Chứng tỏ đường thẳng y = mx - 2m + 1 luôn đi qua một điểm cố định khi m thay đổi.
y=m(x-2)+1
=>m(x-2)-y+1=0
Điểm mà (d) luôn đi qua có tọa độ là:
x-2=0 và 1-y=0
=>x=2 và y=1
Đúng 1
Bình luận (0)





















