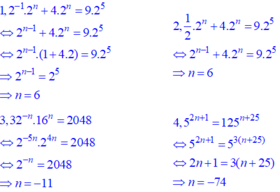Chứng minh 52n+1.2n+2 + 3n+2.2n+1 chia hết cho 38 ( dùng đồng dư)

Những câu hỏi liên quan
1.Chứng minh rằng \(2^{2^{6n+2}}+3⋮19\) với ,mọi n\(\in\)N
2.Chứng minh rằng với n>0 ta có 52n-1.22n-15n+1+3n+1.22n-1 chia hết cho 38
Câu 1:Tìm số dư khi chia 31000 cho 2;5;11;13;17 (giải theo dạng toán đồng dư)Câu 2:(giải theo dạng toán đồng dư). Chứng minh A22225555+ 55552222 chia hết cho 7B32010+52010 chia hết cho 13Câu 3: (giải theo dạng toán đồng dư)Chứng minh: A62n+19n- 2n+1 chia hết cho 17B33n+2+5.23n+1chia hết cho 19C212n+1+172n+1+15 không chia hết cho 19
Đọc tiếp
Câu 1:Tìm số dư khi chia 31000 cho 2;5;11;13;17 (giải theo dạng toán đồng dư)
Câu 2:(giải theo dạng toán đồng dư).
Chứng minh A=22225555+ 55552222 chia hết cho 7
B=32010+52010 chia hết cho 13
Câu 3: (giải theo dạng toán đồng dư)
Chứng minh: A=62n+19n- 2n+1 chia hết cho 17
B=33n+2+5.23n+1chia hết cho 19
C=212n+1+172n+1+15 không chia hết cho 19
1.2n-9 chia hết cho n+3
2.4n+5 chia hết cho n-6
3.7+3n chia hết cho n+1
4.12 chia hết cho n-5
5.-15 chia hết cho n+6
1) 2n - 9 chia hết cho n+3
\(\Rightarrow2n-9=2n+6-15=2\left(n+3\right)-15\)chia hết cho n + 3
Vậy n + 3 thuộc Ư(15)
n + 3 \(\in\)Ư(15) = { 1,3,5,15,-1,-3,-5,-15}
Lập bảng ra nhé
2) \(4n+5=4n-24+29=4\left(n-6\right)+29⋮n-6\)
Vậy n-6 \(\in\)Ư(29)
n - 6 \(\in\){ 1,29,-1,-29}
n \(\in\){ 7 ; 35 ; 5 ; -23}
Đúng 0
Bình luận (0)
3) \(3n+7=3n+3+4=3\left(n+1\right)+4⋮n+1\)
=> n + 1 \(\in\)Ư(4)
n + 1 \(\in\){ 1,2,4,-1,-2,-4}
Sau đó bạn lập bảng rồi tìm n
4) 12 chia hết cho n-5 nên n - 5 \(\in\)Ư(12)
=> n - 5 \(\in\){ 1,2,3,4,6,12,-1,-2,-3,-4,-6,-12}
5) -15 chia hết cho n + 6
=> n + 6 thuộc Ư(-15)
Hay n + 6 thuộc { 1,3,5,15,-15,-3,-5,-1}
Đúng 0
Bình luận (0)
Chứng minh 1n+2n+3n+4n ⋮ 5 ⇔ n không chia hết cho 4(với mọi số tự nhiên n khác 0)
gợi ý : 1 đồng dư 1 (mod 5)
4 đồng dư -1(mod 5)
Tìm số nguyên n, biết
1
)
2
−
1
.2
n
+
4.2
n
9.2
5
2
)
1
2
.2
n
+
4.2
n
9.2
5
3...
Đọc tiếp
Tìm số nguyên n, biết
1 ) 2 − 1 .2 n + 4.2 n = 9.2 5
2 ) 1 2 .2 n + 4.2 n = 9.2 5
3 ) 32 − n .16 n = 2048
4 ) 5 2 n + 1 = 125 n + 25
Cho m, n thuộc Z.
Chứng minh rằng :
1. m.n(m^4-m^4) chia hết cho 30.
2.2n(16-n^4)chia hết cho 30.
1, Câu hỏi của Trịnh Hoàng Đông Giang - Toán lớp 8 - Học toán với OnlineMath
2, \(2n\left(16-n^4\right)=2n\left(1-n^4+15\right)=2n\left(1-n^2\right)\left(1+n^2\right)+30n=2n\left(1-n\right)\left(1+n\right)\left(n^2-4+5\right)+30n\)
\(=-2n\left(n-1\right)\left(n+1\right)\left(n^2-4\right)+10n\left(n-1\right)\left(n+1\right)=-2n\left(n-1\right)\left(n+1\right)\left(n-2\right)\left(n+2\right)+10n\left(n-1\right)\left(n+1\right)\)
Vì n(n-1)(n+1)(n-2)(n+2) là tích 5 số nguyên liên tiếp nên chia hết cho 3;5
Mà (3,5) = 1
=> n(n-1)(n+1)(n-2)(n+2) chia hết cho 15
=> -2n(n-1)(n+1)(n-2)(n+2) chia hết cho 2.15 = 30 (1)
Vì n(n-1)(n+1) là tích 3 số nguyên liên tiếp nên chia hết cho 3
=>10n(n-1)(n+1) chia hết cho 10.3 = 30 (2)
Từ (1) và (2) => \(-2n\left(n-1\right)\left(n+1\right)\left(n-2\right)\left(n+2\right)+10n\left(n-1\right)\left(n+1\right)⋮30\) hay \(2n\left(16-n^4\right)⋮30\left(đpcm\right)\)
Đúng 0
Bình luận (0)
chứng minh \(70\times27^{1001}+31\times38^{101}\)chia hết cho 13 (giải bằng 2 cách (trong đó có 1 cách dùng đồng dư)
a)cho a,b là 2 số tự nhiên. Số a chia 5 dư 1, số b chia 5 dư 2. Chứng minh rằng ab chia 5 dư 2
b) số a gồm 31 chữ số 1, số b gồm 38 chữ số 1. Chứng minh rằng ab-2 chia hết cho 3
Chứng minh rằng với mọi số tự nhiên n thì 52n+752n+7 chia hết cho 8
Đọc tiếp
Chứng minh rằng với mọi số tự nhiên n thì chia hết cho 8
Ta có 52n+7 = 25n+7
Lại có 25:8 dư 1 => 25n:8 dư 1n
Mà 1n = 1 => 25n chia 8 dư 1
=> 25n+7 chia 8 dư 1+7 hay dư 8
Mà 8⋮8 => đpcm
Đúng 0
Bình luận (0)