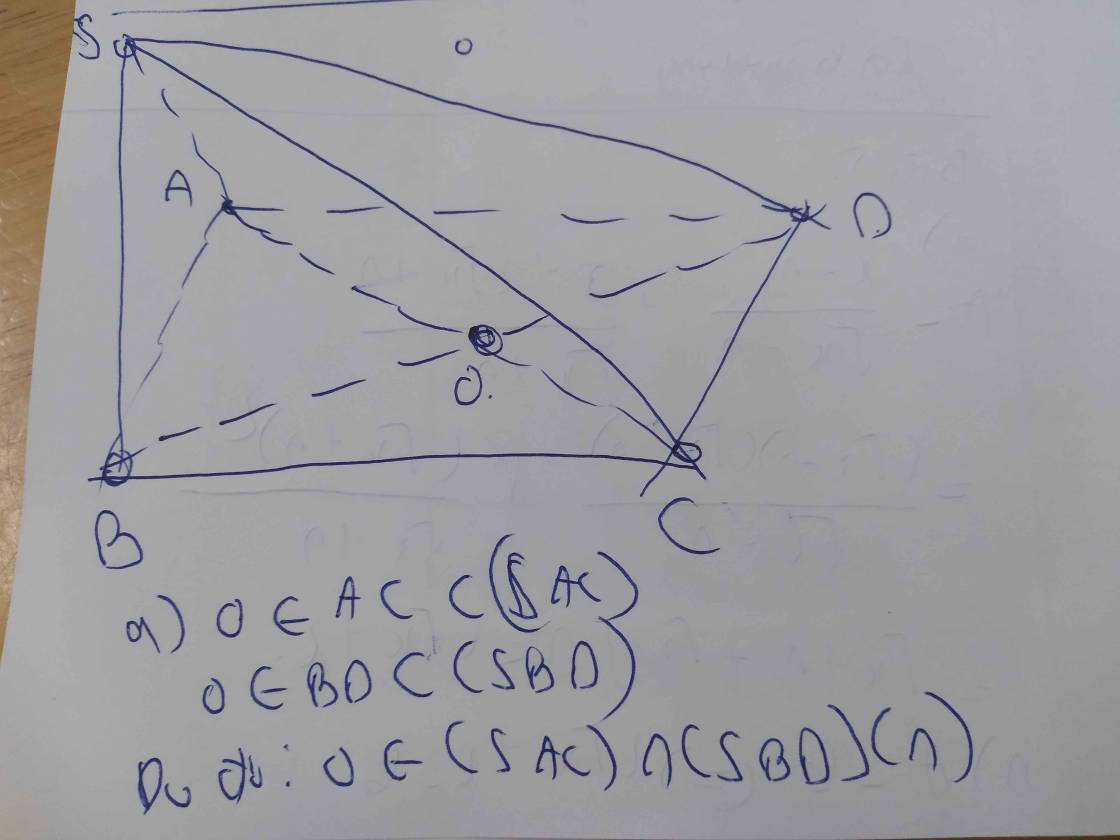
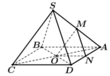
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M,N,P lần lượt là trung điểm của AB,AD và SO.
a, tìm giao điểm của SC với mặt phẳng MNP
b, CMR MN song song với mặt phẳng SBD
c, Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng MNP